COMPUTATIONAL PHILOSOPHY OF SCIENCE
1993 The MIT Press
Massachusetts Institute of Technology
Cambridge, Massachusetts
---------
FILOSOFÍA COMPUTACIONAL DE LA CIENCIA
Traducción en elaboración*: Giovanna Winchkler y
Juan Magariños de Morentin
[Para el Seminario: "En el principio era la imagen"]
[xi] 1
Prefacio
"Filosofía computacional de la ciencia" va a sonar para algunos oídos como la empresa más antinómica en la filosofía, después de la ética de los negocios. Sin embargo, puede iluminar los problemas filosóficos más importantes, concernientes a la estructura y desarrollo del conocimiento científico, aproximando ideas y técnicas del campo de la IA Este libro usa PI, un programa de computación para resolución de problemas e inducción, con el fin de ilustrar la pertinencia de las ideas computacionales a los problemas que se vinculan con el descubrimiento, evaluación y aplicación de las teorías científicas.
La primera parte del libro se ocupa de los modelos computacionales del pensamiento científico y debería llamar la atención de quienes estén interesados en la IA y en la psicología cognitiva, al igual que la de los filósofos. Los capítulos subsiguientes se dedican a problemas filosóficos más tradicionales, vinculados con la relación entre cómo se realiza el razonamiento y cómo debería realizarse, con la verdad, con la justificación de los métodos científicos y con la diferencia entre ciencia y seudociencia. Se aplican algunas conclusiones generales sobre la naturaleza del método científico a los campos particulares de la psicología y la IA El libro concluye con un capítulo altamente especulativo acerca de lo que podrían añadir los modelos computacionales a nuestra comprensión de dos aspectos clave del proceso de investigación: las interrelaciones de la teoría y el experimento, y la importancia de la racionalidad grupal en la ciencia.
He tratado de que este libro fuese accesible a una lectura de carácter interdisciplinario, aclarando los términos filosóficos y computacionales a medida que van surgiendo. Con el objeto de proporcionar los conocimientos básicos a los lectores de diferentes ámbitos sin interrumpir la argumentación, el apéndice 1 contiene cuatro tutoriales que brindan indispensables introducciones filosóficas, computacionales y psicológicas. Cada capítulo concluye con un resumen de sus propuestas más importantes.
Este libro se presenta con la esperanza de que se lea sin categorizaciones arbitrarias acerca de lo que sea filosofía, IA o psicología y con la convicción de que sólo a través de la cooperación interdisciplinaria puede alcanzarse una comprensión del razonamiento científico.
[xiii]
Agradecimientos
Este libro ha contado con la ayuda de muchas personas e instituciones. Lo inicié cuando era Profesor Asociado de Filosofía en la Universidad de Michigan-Dearborn; estoy agradecido por la libertad que allí me concedieron mis colegas. Gran parte del trabajo se realizó mientras estuve también asociado en el Cognitive Science Program de la Universidad de Michigan, Ann Arbor, la cual brindó distintos tipos de apoyo. El libro se completó usando las excelentes instalaciones del Cognitive Science Laboratory en la Universidad de Princeton, donde ahora me encuentro realizando investigación interdisciplinaria como parte del Human Information Processing Group.
En el período durante el cual muchas ideas de este libro se desarrollaron, tuve la fortuna de colaborar con John Holland, Keith Holyoak y Richard Nisbett en nuestro libro de 1986: Induction: Processes of Inference, Learning, and Discovery. Algunos temas desarrollados aquí se esbozaron de manera preliminar en él. Tengo una deuda especial con Keith Holyoak, ya que el sistema de procesamiento PI, cuyas implicaciones filosóficas y aplicaciones se discuten extensamente aquí, es un proyecto en colaboración con él. Estoy agradecido a Richard Nisbett por haberme introducido en el trabajo de la psicología cognitiva, y a John Holland por supervisar mi M.S. en ciencia de la computación.
Los primeros borradores de este libro recibieron valiosos comentarios de Paul Churchland, Robert Cummins, Daniel Hausman, Stephen Hanson, Gilbert Harman, Ziva Kunda, Richard Nisbett y Ian Pratt. Estoy particularmente agradecido a Lindley Darden por sus detallados comentarios acerca de dos borradores.
Durante los años en que se desarrolló este libro, he sido beneficiado con subsidios por parte de la National Science Foundation, la Sloan Foundation, la Systems Development Foundation, la Basic Research Office del Army Research Institute for Behavioral and Social Science, y la McDonnell Foundation.
Algunas secciones del libro provienen de artículos previamente publicados. Agradezco a los correspondientes editores por el permiso para usar el siguiente material:
(Falta el listado de ese material, p. xiv)
[1]
Capítulo 1La computación y la filosofía de la ciencia
La epistemología sin contacto con la ciencia se convierte en un esquema vacío. La ciencia sin epistemología, si es que puede concebirse, es primitiva y confusa. (Albert Einstein, 1949, pp. 683ss)
1.1. Un nuevo enfoque
La filosofía de la ciencia y la IA tienen mucho para aprender una de otra. Las principales preguntas para las que una investigación multidisciplinaria puede ser de utilidad, son:
¿Qué son las teorías científicas?
¿Qué es explicación científica y resolución de problemas?
¿Cómo se descubren y evalúan las teorías?
¿Cómo adquieren significado los conceptos teóricos?
¿Cuáles son los roles de la teorización y la experimentación en el proceso de la investigación científica?
¿Cómo pueden los estudios que describen cómo se hace la ciencia tener importancia para los juicios normativos sobre cómo debe hacerse?
Este libro presenta un conjunto completo de respuestas a estas preguntas en un marco computacional. He aquí un esquema preliminar de lo que se va proponiendo en los capítulos siguientes:
1. Las teorías son estructuras complejas de datos en los sistemas computacionales; consisten en paquetes muy organizados de reglas, conceptos y soluciones a problemas.
2. Explicación y resolución de problemas son procesos computacionales mediatizados por las reglas, conceptos y soluciones a los problemas que pueden constituir las teorías.
3. El descubrimiento y evaluación de las teorías son subprocesos que se desencadenan en el contexto de la explicación y la resolución de problemas.
4. Los conceptos teóricos son significativos porque se generan en los procesos de [2] descubrimiento y por sus conexiones con otros conceptos.
5. La teorización y la experimentación cumplen roles complementarios en la investigación científica, sin ser dominante ninguno de los dos.
6. Los estudios que describen cómo se hace la ciencia pueden brindar una contribución esencial a la decisión de cómo debe hacerse la ciencia.
En los capítulos subsiguientes se irán concretando estas vagas propuestas. Para precisarlas, describiré un programa de IA para resolución de problemas e inducción y mostraré cómo su operación ayuda a ilustrar los procesos mediante los cuales se construyen y usan las teorías científicas. Demostraré que usando los recursos de la IA, pueden desarrollarse interpretaciones filosóficas más ricas de la resolución científica de problemas, del descubrimiento y de la justificación, que las que son posibles con las técnicas tradicionales de la lógica y de la teoría de conjuntos. No pretendo haber resuelto los múltiples y difíciles problemas concernientes a temas como la explicación y la justificación, a los que me dedico aquí; espero mostrar, en cambio, que el enfoque computacional ofrece ideas y técnicas para representar y usar el conocimiento, que sobrepasan las habitualmente empleadas por los filósofos. Antes de sumergirme en los detalles computacionales, quiero situar esta empresa a la que me estoy refiriendo como "filosofía computacional de la ciencia", en relación a dominios más familiares.
1.2. Inteligencia artificial, psicología y filosofía histórica de la ciencia
La inteligencia artificial (IA) es la rama de la ciencia de la computación que procura lograr que las computadoras realicen tareas inteligentes. En sus cortas tres décadas de vida, la IA ha desarrollado numerosas herramientas computacionales para describir la representación y el procesamiento de la información. Los psicólogos cognitivistas han encontrado que estas herramientas son valiosas para desarrollar teorías acerca del pensamiento humano. De modo semejante, la filosofía computacional de la ciencia puede usarlas para describir la estructura y desarrollo del conocimiento científico.
En gran medida, los intereses de la IA, la psicología cognitiva y la filosofía computacional de la ciencia, se superponen, si bien la filosofía tiene un interés mayor en los temas normativos que los otros dos campos. Debemos distinguir entre los temas descriptivos vinculados a cómo piensan los científicos y los temas normativos, vinculados a cómo deben pensar los científicos. La psicología cognitiva se dedica a la investigación empírica de los procesos mentales y los temas normativos le interesan sólo en la medida en que contribuyan a caracterizar el alejamiento de la gente de las normas asumidas (ver Nisbett y Ross, 1980, para un panorama reciente). De la misma manera, la IA entendida como modelización cognitiva puede confinarse a lo descriptivo más que a lo normativo. Sin embargo, la IA se relaciona a veces también con el mejoramiento del desempeño de la gente y entonces le interesa lo que es óptimo y normativo. [3] La discusión de las cuestiones normativas es inevitable en filosofía de la ciencia, aunque veremos en el capítulo 7, que los problemas descriptivos y los normativos están íntimamente relacionados.
En general, la investigación actual en IA se divide en dos campos que han sido caracterizados pintorescamente como "pulcros" ("neats") y "desprolijos" ("scruffies"). La distinción se basa en gran medida en actitudes referentes a la importancia de la lógica formal para comprender la inteligencia. Los pulcros, como John McCarty (1980) y Nils Nilsson (1983), ven la lógica como esencial para la IA, la cual de este modo consiste principalmente en la construcción de sistemas formales en los cuales la deducción lógica es el proceso central. Por el contrario, la IA desprolija, representada por ejemplo por Marvin Minsky (1975) y Roger Schank (1982), asume un enfoque mucho más psicológico al sostener que es más probable que la IA tenga resultados provechosos si evita el rigor de la lógica formal y, en cambio, investiga las estructuras y los procesos más variados hallados en el pensamiento humano. Usando el término que aplican los programadores de computación para designar un programa complejo y asistemáticamente armado, Minsky señala que el cerebro es un "kluge" ([o "kludge"], inelegante pero eficaz). Un tercer enfoque incidente en la IA, el de los sistemas de producción de Newell y Simon (1972), cae en algún lado entre los campos pulcros y desprolijos. Los psicólogos van desde los pulcros que enfatizan el papel de la lógica en el pensamiento (Braine, 1978; Rips, 1983) hasta los desprolijos que niegan que la lógica sea en absoluto central (Johnson-Laird, 1983; Cheng et al., 1986).
La filosofía tiene también sus pulcros y sus desprolijos. Nunca nadie fue más pulcro que los positivistas lógicos, que usaron las técnicas de la lógica formal para analizar la naturaleza de las teorías y otras cuestiones fundamentales. No es entonces sorprendente que los filósofos inclinados hacia lo formal muestren un interés creciente en empeños de la IA tales como el análisis algorítmico y la programación lógica (Glymour, Kelly y Scheines, 1983). Pero esta tendencia refleja la relación solamente entre la IA pulcra y la filosofía de la ciencia pulcra. Dado que toda realización en computadora requiere formalización y que ésta fue la marca identificadora de los positivistas lógicos, uno podría suponer que todos los enfoques de la IA caen dentro del campo positivista. Sin embargo, tal conclusión implica un lamentable desprecio por los recursos intelectuales de la IA.
En las décadas de 1950 y de 1960, la filosofía de la ciencia asistió a una rebelión contra las interpretaciones lógico positivistas de la ciencia, encabezada por escritores como Hanson (1958) y, especialmente, Kuhn (1970b). (En el tutorial A, apéndice 1, puede verse un esquema de los desarrollos de la filosofía de la ciencia.) Los críticos sostuvieron que el énfasis positivista en los modelos formales los había apartado cada vez más de la práctica de la ciencia corriente. Muchos filósofos de la ciencia han adoptado desde entonces una metodología que evita la formalización, ofreciendo en lugar de ella consideraciones menos precisas de los métodos de los científicos, basándose en estudios de casos históricos. Kuhn, por ejemplo, hizo un uso abundante de ejemplos como el de la teoría del oxígeno de Lavoisier y la teoría de la relatividad de Einstein, para vertebrar su interpretación del desarrollo de la ciencia.
[4] La filosofía histórica de la ciencia ha aportado una interpretación mucho más rica y sutil de la naturaleza de la ciencia, que la que se pudo desarrollar en el marco de los positivistas lógicos. Pero le ha faltado uno de los rasgos más atractivos del programa positivista: el rigor analítico. Kuhn describió las revoluciones científicas como la superación de un paradigma por otro, pero dejó notoriamente impreciso el concepto central de paradigma. De modo semejante, el influyente trabajo de Laudan (1977) sobre la ciencia como actividad de resolución de problemas, nunca dijo mucho acerca de la naturaleza de la resolución de problemas.
La filosofía computacional de la ciencia, que este libro coloca en la intersección de la IA desprolija y la filosofía histórica de la ciencia, puede llenar esas lagunas. Espero mostrar, ofreciendo análisis computacionales detallados de la estructura y desarrollo del conocimiento, que la filosofía postpositivista de la ciencia puede tener algún rigor en su desprolijidad.
Tanto Hanson como Kuhn hicieron uso de las ideas de la psicología de la gestalt al desarrollar sus interpretaciones alternativas frente a los testimonios lógico positivistas de la ciencia. La filosofía computacional de la ciencia está aún más estrechamente ligada con la psicología, en virtud del eslabón entre la IA desprolija y la psicología cognitiva actual, que emplea cada vez más los modelos computacionales en cuanto herramientas teóricas. Estos tres campos pueden colaborar en el desarrollo de un análisis computacional acerca de cómo piensan los científicos humanos. Hay investigadores en filosofía de la ciencia e IA que preferirían dejar la psicología fuera de la escena, con lo cual la ciencia algún día sería realizada en verdad por computadoras usando procesos muy diferentes de los usados por los humanos. Pero, al menos por ahora, la ciencia es una empresa humana y la comprensión del desarrollo del conocimiento científico depende de un balance de los procesos de pensamiento de los humanos. Por lo cual la filosofía computacional de la ciencia se solapa tanto con la psicología cognitiva como ésta lo hace con la IA desprolija. Hasta sus prescripciones normativas acerca de cómo conviene hacer ciencia, deberían tomar las limitaciones cognitivas humanas como sus puntos de partida, según el enfoque desarrollado en el capítulo 7.
La filosofía computacional de la ciencia y gran parte de la psicología cognitiva actual emplean modelos computacionales. Pero, ¿por qué? En la próxima sección esbozaré las ventajas metodológicas de usar programas de computación para comprender el pensamiento.
1.3. ¿Por qué escribir programas?
Los programas de computación ofrecen a la psicología cognitiva y a la filosofía computacional de la ciencia al menos tres grandes beneficios: 1) la ciencia de la computación proporciona un vocabulario sistemático para describir estructuras y mecanismos; 2) la implementación de las ideas en un programa ejecutable es una prueba de su coherencia interna; y 3) la ejecución del programa puede proporcionar pruebas [5] acerca de las consecuencias previstas e imprevistas de las hipótesis. La psicología cognitiva actual está empapada de nociones computacionales, tales como búsqueda, activación expansiva (spreading activation), memoria intermedia (buffer), recuperación, etc. El nacimiento de la psicología cognitiva en la década del ‘60 dependió de la metáfora computacional que brindó por primera vez recursos precisos para describir estructuras y procesos internos muy ricos. En la década del ‘70, el campo interdisciplinario de la Ciencia Cognitiva reunió investigadores de diversos ámbitos, todos ellos interesados en comprender la naturaleza de la mente, con la compartida esperanza de que los modelos computacionales ayudarían.
El análisis computacional de la mente depende de estas correspondencias:
|
Pensamiento |
Programa |
|
Estructuras mentales |
Estructuras de datos |
|
Procesos |
Algoritmos |
Los conductistas argumentaron que las especulaciones sobre los contenidos de la mente eran un bagaje metafísico; pero la computadora hizo posible que las estructuras mentales y los procesos supuestos se concretaran, aún cuando el problema de verificar su existencia siga siendo difícil. Puede concebirse un programa como una serie de estructuras de datos junto con una serie de algoritmos que operan mecánicamente con las estructuras de datos. Las estructuras pueden ser muy simples, digamos, una lista de elementos como (1 2 3). O bien, se hacen mucho más complejas, como en el lenguaje de procesamiento de listas LISP, en el cual es fácil crear estructuras consistentes en listas organizadas incrustadas en otras listas. Pueden entonces escribirse algoritmos (procedimientos bien definidos) que operan sobre esas estructuras de datos, creando otras nuevas. (Ver el tutorial C para una introducción rápida al papel de las estructuras de datos y los algoritmos en programación.)
De la misma manera, el enfoque actual más plausible y desarrollado acerca de la mente postula estructuras mentales o representaciones internas acompañadas por procesos para usar tales representaciones (Gardner, 1985). Podemos desarrollar modelos más detallados de la mente escribiendo programas que tengan estructuras de datos correspondientes a las representaciones supuestas y algoritmos que correspondan a su vez a los procesos supuestos. Para que pueda ejecutarse en la computadora, el programa ha de ser explícito, y el ejercicio de elaboración de las estructuras y los procesos coordinados, llevará, en general, al desarrollo de un modelo más rico y más complejo que el posibilitado por la especulación no asistida por computadora. Es mucho lo que se puede aprender acerca de un dominio científico cuando se lo intenta analizar dentro de un complejo esquema de representación. Al respecto, el capítulo 2 señala que el enfoque computacional pone a disposición estructuras de datos más ricas que las que se tomarían en cuenta de otro modo. Los filósofos en particular, han tendido a restringir sus discusiones a un conjunto más limitado de estructuras (oraciones o proposiciones) y a una clase de procesos más limitado (la deducción). Como veremos, [6] propiciar la investigación de procesos menos restringidos, como los que subyacen al descubrimiento científico, es más propio de la computación que de la deducción, haciendo posible la investigación de procesos menos restringidos, como los que subyacen al descubrimiento científico.
Dado que se supone que los procesos mentales son computacionales, la computadora puede ser una herramienta más poderosa para la psicología que para la economía o la meteorología, que usan simulaciones débiles, frente a las simulaciones fuertes de la psicología. En una simulación débil, la computadora funciona como un dispositivo de cálculo que saca las consecuencias de las ecuaciones matemáticas que describen los procesos simulados. Una computadora puede simular eficazmente un ciclo de negocios o un huracán, pero nadie afirma que tenga, de hecho, depresión económica o fuertes vientos. En una simulación fuerte, la simulación misma semeja el proceso simulado. Por ejemplo, un túnel de viento usado para estudiar la aerodinámica de los automóviles es una simulación fuerte, puesto que el flujo de aire sobre el vehículo en el túnel es similar al flujo de aire sobre el vehículo en una autopista. Por el contrario, un modelo computado de la aerodinámica del automóvil sería solamente una simulación débil. Mientras que para la mayoría de los campos la computadora proporciona sólo simulaciones débiles, la psicología tiene la posibilidad de contar con simulaciones fuertes, si la teoría computacional de la mente es correcta.
Desde luego que la mera caracterización de las estructuras de datos y procesos en términos computacionales no nos dice cómo opera la mente. Pero el solo hecho de conseguir que el programa funcione, ofrece una prueba de varias clases. Algunos psicólogos no computacionales tienden a suponer que nada puede programarse, lo cual no es más creíble que pensar, como lo hacen algunos científicos de la computación, que un experimentador inteligente puede obtener cualquier dato psicológico. Un programa de computación debe tener, para que pueda funcionar, por lo menos una interrelación coherente de las estructuras y los algoritmos. Además, la amenaza de la explosión combinatoria impone una severa restricción sobre la factibilidad de los programas: si el programa requiere aumentar exponencialmente el tiempo de ejecución, agotará muy pronto los recursos de las computadoras más poderosas. De manera que el mismo desarrollo de una simulación en computadora ofrece una valiosa prueba de la coherencia interna de un conjunto de ideas.
Un modelo psicológico debería ser más que internamente coherente: queremos que dé cuenta de los datos experimentales de cómo piensa la gente. Algunas veces, si el modelo es complejo, no es fácil ver cuáles son sus consecuencias. Los modelos cognitivos, como muchos otros modelos de las ciencias sociales suelen proponer numerosos procesos interactivos. El programa de computación permite que el investigador vea si el modelo tiene todas las consecuencias, y sólo esas, que se espera que tenga. La comparación de estas consecuencias con las observaciones experimentales brinda un modo de validar el modelo con mucho mayor detalle de lo que podrían permitir los cálculos con lápiz y papel. La filosofía computacional de la ciencia puede aprovechar los mismos beneficios de la formación de modelos y de la prueba de modelos que los que proporciona la IA a la psicología cognitiva.
[7]
1.4. PsicologismoPor lo tanto, la filosofía computacional de la ciencia está íntimamente vinculada con la psicología cognitiva y la IA. Si las ciencias cognitivas sugieren una revisión de las consideraciones clásicas acerca de la estructura y el desarrollo del conocimiento, se esperaría de esas posiciones una significación epistemológica inmediata. Pero a causa de la ruptura entre filosofía y psicología producida en la segunda mitad del siglo diecinueve, la mayoría de los filósofos desarrollaron posiciones epistemológicas independientes por completo del trabajo de los psicólogos empíricos. La mezcla de discusiones filosóficas y psicológicas se ha rotulado como "psicologismo".
La razón más fundamentada del temor que tienen los filósofos de una asociación con la psicología, es que los intereses normativos de la filosofía se diluirían o abandonarían. Considérese el siguiente argumento contra el psicologismo, semejante a los de Frege (1964) y Popper (1972). La epistemología, dice el argumento, está tan desvinculada de la psicología como lo está la lógica. La psicología describe qué inferencias realiza la gente, pero a la lógica le interesa qué inferencias debería hacer la gente; lo normativo, más que lo descriptivo. Del mismo modo, la epistemología es la teoría normativa del conocimiento objetivo y no necesita tener en cuenta la naturaleza de los sistemas de creencias en los individuos tal como lo determina la psicología. Las proposiciones u oraciones que los expresan, pueden ser las conclusiones de los argumentos y pueden escribirse en libros que están a disposición del público. El examen de la estructura de los sistemas de creencias individuales sería sólo para estimular una clase de subjetivismo que abandona los nobles intereses tradicionales de la epistemología, la justificación y la verdad, por un vago relativismo. (El relativismo es la posición filosófica que sostiene que la verdad es relativa y puede variar de persona a persona o en el tiempo, sin estándares objetivos.)
Sin embargo, un interés por la psicología no necesita engendrar el escepticismo epistemológico. Haack (1978) recomendó un psicologismo débil, según el cual la lógica es prescriptiva de los procesos mentales. Esta posición se diferencia tanto del antipsicologismo, que es el enfoque de Frege/Popper por el cual la lógica nada tiene que ver con los procesos mentales, como del psicologismo fuerte, que sostiene que la lógica es a la vez descriptiva y prescriptiva respecto de los procesos mentales. ("Débil" y "fuerte" no tienen aquí relación con su uso en la sección anterior referente a la simulación.) El psicologismo débil usa a la psicología empírica como punto de partida, ya que presupone una consideración empírica de los procesos mentales acerca de los cuales cabe ser prescriptivo. Pero va más allá de la mera descripción de los procesos mentales corrientes, para considerar qué clase de prácticas inferenciales son normativamente correctas. De este modo, el psicologismo débil puede evadir la acusación de relativismo, motivo principal de la resistencia a admitir lo relevante que es la psicología para la epistemología. Tal evasión requiere, sin embargo, dar cuenta de cómo las cuestiones empíricas descriptivas conciernen a las cuestiones prescriptivas, aunque no ofrezcan respuestas completas.
[8] El conocimiento es tanto privado como público, alojándose en los cerebros de pensadores particulares, pero también está sujeto a la comunicación y evaluación intersubjetiva. El psicologismo débil se propone capturar estos dos aspectos. La verdadera prueba entre psicologismo y antipsicologismo consiste en ver qué sistema puede desarrollar una propuesta comprehensiva y rica acerca del conocimiento humano. Puede considerarse a este libro como un intento computacionalmente orientado para describir algunos resultados posibles de un programa de investigación psicológica débil. Otros intentos afines incluyen la naturaleza epistemológica de Quine (1969), la epistemología genética de Piaget (1970), la epistémica de Goldman (1978, 1986) y la epistemología evolutiva de Campbell (1974). Esta última se comenta en el capítulo 6.
Comparto con estos autores la concepción de que el método filosófico debería ser más afín con la construcción de teorías en la ciencia, que con la clase de análisis conceptual que ha predominado en gran parte de la filosofía del siglo veinte. No se realizarán análisis precisos de conceptos individuales porque hay bases para dudar de si tales análisis deban hacerse (ver secciones 2.3.1 y 4.4) y porque resulta mucho más interesante la empresa mayor consistente en describir las conexiones sistemáticas entre procesos como la explicación y la formación de hipótesis.
1.5. Plan general
La exploración de la filosofía computacional de la ciencia comienza en el próximo capítulo, con una exposición de las estructuras y procesos básicos relacionados con una comprensión del conocimiento científico. El programa PI de IA proporciona un ejemplo concreto de cómo puede organizarse y usarse el conocimiento en la resolución de problemas. El capítulo 3 desarrolla luego una propuesta computacional de la naturaleza de las teorías y explicaciones científicas. El capítulo 4 describe cómo puede implementarse computacionalmente la inferencia abductiva y da cuenta desde ese enfoque, de diversas clases de descubrimientos científicos. Expone también cómo pueden formarse y adquirir significado los nuevos conceptos. En el capítulo 5 desarrollo una propuesta para la evaluación de la teoría como inferencia para la mejor explicación y describo su realización en PI. El capítulo 6 usa las ideas sobre descubrimiento y evaluación de teorías desarrolladas en capítulos anteriores, para criticar el modelo darwiniano de desarrollo del conocimiento, que sostienen los epistemólogos evolucionistas. Los tres capítulos que siguen, pasan a las cuestiones normativas. El capítulo 7 elabora un modelo para alcanzar conclusiones normativas a partir de consideraciones descriptivas y en el capítulo 8, este modelo se aplica a los problemas de la justificación de la inferencia para la mejor explicación y a la defensa del realismo científico. El capítulo 9 expone los problemas normativos que se plantean al distinguir ciencia y seudociencia. Finalmente, en el capítulo 10, ofrezco algunas sugerencias especulativas sobre los aportes que la filosofía computacional de la ciencia puede aportar a los problemas vinculados con la relación [9] entre teoría y experimento y el papel de la racionalidad de los grupos en la ciencia. He agregado tres apéndices para poner los detalles que en otro lugar hubiesen distraído la atención del argumento principal. El primero de ellos, consiste en cuatro tutoriales que proporcionan información básica relativa a filosofía de la ciencia, la lógica, la estructuras de datos y algoritmos, y los esquemas. El segundo, brinda un resumen de la estructura del programa de computación PI expuesto en los capítulos 2-5, y el tercero, presenta un ejemplo de funcionamiento de PI.
1.6. Resumen
La filosofía computacional de la ciencia es un intento de comprender la estructura y desarrollo del conocimiento científico en términos de la elaboración de estructuras computacionales y psicológicas. Su objetivo es brindar nuevas propuestas acerca de la naturaleza de las teorías y las explicaciones, y de los procesos que subyacen su desarrollo. Aunque presenta analogías con las investigaciones en IA y psicología cognitiva, difiere de éstas en que tiene una componente esencial normativa.
[11]
Capítulo 2La estructura del conocimiento científico
Este capítulo inicia un análisis computacional del conocimiento científico exponiendo cómo puede representarse y usarse en programas de computación ese conocimiento. La IA ofrece un nuevo conjunto de técnicas para representar diferentes partes del corpus científico, incluyendo leyes, teorías y conceptos. Con el objeto de mostrar concretamente que se necesitan representaciones complejas de estos ingredientes esenciales del conocimiento científico, voy a describir PI, un programa en funcionamiento, para la resolución de problemas y la inducción.
2.1. Estructura y Proceso
En el capítulo anterior vimos que la fuerte influencia de las ideas computacionales en psicología obedece a buenas razones. La IA ha enriquecido a la psicología con una cantidad de nuevas ideas concernientes a las representaciones y los procesos y con una nueva metodología para probar las ideas mediante la simulación por computadora. Este capítulo y otros subsiguientes mostrarán que hay razones igualmente buenas para una aproximación computacional a la epistemología y la filosofía de la ciencia.
El argumento a favor de la relevancia epistemológica de la computación descansa sobre un punto simple pero en extremo importante: no se puede separar estructura de proceso. No podemos discutir sobre la estructura del conocimiento sin prestar atención a los procesos necesarios para usarla. Este punto es familiar para la mayoría de los practicantes de la IA, pero es nuevo para los filósofos, quienes durante este siglo han tenido una perspectiva relativamente simple de la estructura del conocimiento. Desde el trabajo precursor de Frege y Russell, la lógica formal ha sido el modo canónico de descripción de la estructura del conocimiento. En el cálculo de predicados de primer orden, una oración atómica simple como por ejemplo, "Fred está enojado" se representa mediante un predicado y un argumento, como A(f). El uso del cálculo de predicados por parte de la IA, es menos críptico, de manera que la misma oración se representa como enojado (Fred). Las oraciones más complejas se componen usando conectores como y, o, si-entonces, y por cuantificadores como algunos y todos. Por ejemplo, la oración "Todos los criminales están enojados." puede representarse como (para todo x) (si criminal(x) entonces enojado(x)). El cálculo de predicados es potente como punto de partida para representar el conocimiento, pero veremos más abajo que no proporciona suficiente estructura para todos los objetivos del procesamiento. [12] (Los lectores que necesiten una breve introducción al cálculo de predicados podrá consultar el tutorial B.)
La técnica más estudiada para usar el conocimiento es, en la filosofía del siglo XX, la deducción en los sistemas lógicos, en los cuales las reglas de inferencia pueden definirse con precisión. Por ejemplo, el modus ponens es la regla de inferencia que permite la inferencia de q a partir de si p entonces q y de p. Pero un sistema de procesamiento debe contar con algo más que la deducción. Si el sistema es grande, ensamblar la información pertinente en un momento determinado puede ser un gran problema. En los sistemas epistemológicos basados en la lógica, se considera generalmente que un corpus de conocimiento consiste en todas las consecuencias deductivas de un conjunto de enunciados, aún cuando el conjunto de consecuencias fuese infinito. En el caso de los sistemas más realistas, resulta esencial preguntarse ¿qué debemos inferir cuándo? Así, aún en un sistema diseñado para realizar la deducción, necesitamos procesos que tengan en cuenta qué información hay disponible y qué reglas de inferencia resultan apropiadas.
En todo sistema diseñado para el aprendizaje y para la actuación, para la adquisición del conocimiento y para su uso, se necesitan procesos no deductivos. El descubrimiento científico es multifacético y requiere diversos procesos para la generación de los conceptos, la formación de las leyes generales, y la creación de las hipótesis. Estos procesos dependen, como veremos, de complejas representaciones de conceptos y leyes.
Mi compromiso en este libro es con el conocimiento científico. Por lo tanto, la próxima sección discutirá cuáles son las clases de estructuras y de procesos más importantes para caracterizar el conocimiento científico. Luego describiré un amplio sistema de procesamiento, para ilustrar, con mucho mayor detalle, cómo se interrelacionan estructura y proceso.
2.2. Conocimiento científico
Para representar el conocimiento científico, necesitamos hallar una expresión formal para, al menos, tres clases de información: observaciones, leyes y teorías. Los filósofos de la ciencia han discrepado respecto de la importancia relativa de estos aspectos en el desarrollo del conocimiento científico. En una interpretación simple del desarrollo de la ciencia, los científicos comienzan realizando observaciones experimentales y luego las usan para generar leyes y teorías. En otra interpretación, igualmente simple e inconducente, los científicos comienzan con leyes y teorías y realizan predicciones que luego comprueban con las observaciones. En la mayor parte de la práctica científica, sin embargo, hay una acción recíproca de hipótesis y observaciones, en la que nuevas observaciones llevan a nuevas leyes y teorías y a la inversa (ver el capítulo 10). Para describir los procesos de la ciencia computacionalmente, debemos ser capaces de formalizar observaciones, leyes y teorías en estructuras que puedan formar parte de programas de computación. Sostendré, además, que también se requiere usar una representación rica de los conceptos científicos. La formalización es necesaria [13] pero no suficiente para la representación, ya que podríamos formalizar un cuerpo de conocimiento científico según el cálculo de predicados o la teoría de conjuntos, sin representarlo de un modo computacionalmente aplicable. La formalización y la representación deben ir de la mano, poniendo el conocimiento en una forma que pueda procesarse.
La observación particular de que un espécimen, llamémoslo espécimen27, es azul, se puede representar fácilmente en el cálculo de predicados como azul (espécimen27). Hay observaciones más complejas que se refieren a las relaciones entre objetos, a las cuales el cálculo de predicados puede representar mediante más de un argumento. Por ejemplo, la observación de que un espécimen está a la izquierda de otro, se puede representar como izquierda-de (espécimen27, espécimen42). Las relaciones son aún más importantes en la medida en que se agregue, además, información temporal: podemos formalizar la información de que el espécimen 27 era azul en el tiempo t, escribiendo azul (espécimen27, t). De esta manera, el cálculo de predicados aparece como un recurso excelente para representar observaciones, en especial cuando se trata de relaciones. Toda representación del conocimiento científico debe ser capaz de distinguir entre x a la izquierda de y, e y a la izquierda de x, cuyo cálculo de predicados se realiza muy cómodamente, mediante el contraste de izquierda de (x, y) con izquierda de (y, x).
La ciencia obviamente realiza algo más que coleccionar observaciones. Un objetivo central es organizar las observaciones mediante leyes. En física pueden ser muy generales, como la ley según la cual dos objetos cualquiera tienen una fuerza gravitacional mutua. En las ciencias sociales y en gran parte de la física del siglo XX, es común hablar de efectos más que de leyes, indicando una relación estadística más que la plena generalidad. Las leyes generales pueden representarse naturalmente mediante expresiones cuantificadas en el cálculo de predicados. Por ejemplo, la ley elemental según la cual el cobre conduce la electricidad se escribe como (para todo x) (si cobre(x) entonces conduce-electricidad(x)). Puede parecer entonces, que el cálculo de predicados es todo lo que necesitamos también para las leyes.
Pero esta conclusión desatiende el punto importante mencionado más arriba, acerca de los procesos. Si todo lo que quisimos hacer con las leyes era usarlas en las deducciones lógicas, entonces el cálculo de predicados puede estar bien. Pero las leyes pueden jugar muchos otros papeles importantes. Las leyes se descubren usando observaciones, sirven para predecir nuevas observaciones, ayudan mucho en la resolución de problemas y en la explicación, y se explican mediante teorías. Para funcionar en todos estos procesos, es útil darles a las leyes una representación más compleja, tal como la que se usó para las reglas del sistema PI discutido más abajo.
Desde un punto de vista lógico, las teorías semejan leyes generales. La teoría de la gravitación de Newton, por ejemplo, dice que entre cualesquiera dos cuerpos hay una fuerza. Esto puede representarse mediante la regla Si x es un cuerpo e y es un cuerpo, entonces hay una fuerza z entre x e y. Pero las teorías difieren de las leyes tanto en sus orígenes como en sus roles explicativos. Mientras las leyes son generalizaciones a partir de observaciones, las teorías se evalúan mostrando su capacidad de explicar las leyes (ver capítulo 5). Además, como las teorías van más allá de lo que se observa, [14] para postular entidades tales como electrones, quarks y
genes, no pueden descubrirse del modo empíricamente directo
en que se pueden descubrir en cambio las leyes. Dado que las teorías cumplen diferentes papeles, pueden necesitar una clase más rica de representación para poder funcionar en diferentes procesos. Podemos necesitar, por ejemplo, seguir las huellas del éxito en la explicación de una teoría para evaluarla en comparación con otras teorías.
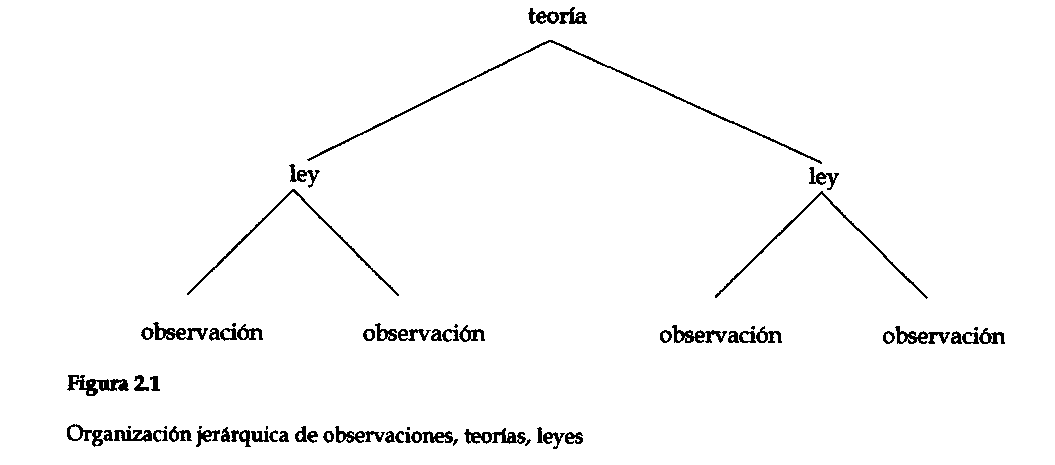
El encuadre general de la estructura del conocimiento científico que estoy proponiendo aquí es corriente en la filosofía de la ciencia actual. Tiene tres niveles, consistentes en: observaciones, observaciones que se generalizan como leyes, leyes que son explicadas como teorías. En términos más simples, la estructura resultante aparece como la que se representa en la figura 2.1. Un ejemplo concreto es una teoría de la luz, tal como la teoría de partículas de Newton o la teoría de las ondas que la reemplazó en el siglo XIX. Estas teorías estaban destinadas a explicar leyes generales tales como que la luz se refleja y se refracta de determinadas maneras, lo que, a su vez, se basaba en observaciones particulares. De modo semejante, los psicólogos proponen teorías acerca de cómo la gente procesa la información, con el objeto de explicar efectos experimentales, que son generalizaciones estadísticas a partir de los resultados observados de los experimentos. (Los críticos de este encuadre de los tres niveles han mantenido que toda observación está "cargada de teoría"; ver la sección 5.7).
La representación de las observaciones, leyes y teorías requiere el uso de predicados como azul, cobre, o electrón. Desde la perspectiva del cálculo de predicados, no hay nada misterioso sobre estos predicados: no son más que marcas sobre el papel, simples unidades sintácticas. (Los lógicos distinguen entre sintaxis, semántica y pragmática. La sintaxis se refiere a las propiedades que tienen los símbolos en virtud de su forma. La semántica se refiere a las relaciones de los símbolos con el mundo y la pragmática trata del uso de los símbolos. Ver Morris, 1938.) Desde un punto de vista semántico, los predicados parecen ser directos, porque la teoría de modelos de Tarski proporciona una semántica para el cálculo de predicados, bajo la forma de una definición de verdad (ver [15] tutorial B). Los predicados están asociados con conjuntos de objetos en un dominio, interpretados como aquellos objetos respecto de los cuales el predicado es verdadero. Sin embargo, veremos en el capítulo 4 que la semántica teórico-modélica es inadecuada como teoría del significado de los predicados científicos.
Los científicos son más conscientes del valor de los conceptos que los lógicos. Sin conceptos apropiados, la formación de leyes y teorías útiles es imposible. Por ejemplo, Einstein e Infeld (1938, p.133) incluyen la siguiente exclamación en su exposición sobre el concepto físico de campo: "¡Cuán difícil sería descubrir estos hechos sin el concepto de campo! La expresión para una fuerza que actúa entre un cable por el cual fluye la corriente y un polo magnético, es muy complicada. En el caso de dos solenoides [bobinas de cable], tendríamos que investigar la fuerza con la cual actúan dos corrientes, la una sobre la otra. Y si lo hacemos con la ayuda del campo, advertimos inmediatamente el carácter de todas esas acciones en el momento en que se ve la similitud entre el campo del solenoide y el de la barra imantada." Para entender la importancia de los conceptos en esta clase de descubrimiento y en el pensamiento científico en general, resulta necesaria una representación de los conceptos más rica que los meros predicados. El capítulo 4 en particular describirá cómo el desarrollo de los conceptos teóricos exige que los conceptos tengan una estructura interna rica.
2.3. Estructura y Proceso en PI
Con el objeto de tratar más concretamente la importancia de representaciones ricas, esbozaré ahora un programa de IA llamado PI, que simboliza "proceso de inducción" y se pronuncia "pie". PI ejecuta, en el lenguaje de programación LISP, un modelo general de resolución de problemas y de inferencia inductiva, desarrollado en colaboración con el psicólogo cognitivista Keith Holyoak. La intención, al describir PI, no es proponerlo como lenguaje canónico para hacer ciencia; se describirán sus limitaciones. Tampoco se supone que PI constituya en sí mismo una solución a la multitud de difíciles problemas que hay en filosofía de la ciencia en relación con la explicación, la justificación, etc. Lo que presento aquí es un ejemplo de cómo interactúan representación y proceso y cómo se puede comenzar a desarrollar en un marco computacional, una interpretación general integrada del descubrimiento científico y la justificación. Más descripciones acerca de las operaciones de PI pueden hallarse en otros trabajos (Holland et al., 1986; Thagard y Holyoak, 1985); los apéndices 2 y 3 contienen información mucho más detallada sobre la implementación de PI en LISP.
2.3.1. Representación del conocimiento
PI representa resultados particulares de observaciones e inferencias mediante mensajes, que son como las oraciones en el cálculo de predicados y lo que se denomina [16] "hechos" en los sistemas de producción. Un mensaje es una lista que incluye la siguiente información: predicado, argumento, valor de verdad, fiabilidad y nombre del mensaje. Por ejemplo, la observación de que el planeta Marte es rojo está representada por la lista (rojo (Marte) verdad 1). Una estructura similar puede también representar hipótesis simples. La información de que por hipótesis Marte pueda estar desprovisto de vida podría representarse por la lista (tiene-vida (Marte) se proyecta como falso .7 hipótesis-26). Además de los obvios valores de verdad verdad y falso, PI permite proyectar otros más como tanteo. El número .7 indica cuánta confianza tiene el sistema en el mensaje y el nombre del mensaje puede usarse para almacenar información adicional, por ejemplo, sobre la evidencia de las hipótesis. Así, los mensajes de PI, aunque comiencen con una estructura que proviene del cálculo de predicados, añaden más información, la cual jugará un papel importante en la resolución de problemas y la inferencia inductiva.
Las leyes están representadas por reglas, que son enunciados
si-entonces, como Si x es cobre entonces x conduce electricidad. Aún
más que para los mensajes, las reglas resultan útiles para añadir mucha más
estructura que la que podría tener un enunciado del cálculo de predicados.
Para empezar, queremos darle nombre a las reglas, para poder realizar un
seguimiento de sus éxitos y fracasos. Los éxitos y fracasos se resumen en una
cantidad llamada fuerza, que en PI es un número entre 0 y 1. Como
podremos ver abajo, es importante para la resolución de problemas que las
reglas estén asignadas a los conceptos; así, el perfil completo de la regla
anterior sobre el cobre, podría ser
Los programadores de LISP reconocerán esto como una lista de propiedad del átomo Regla-22. Los programadores de Pascal lo van a considerar como un registro con varios campos. Los programadores de Basic y Fortran tendrán que verlo como una clase de ordenamiento más complejo de lo que están acostumbrados a usar. Los lógicos denominan, en general, a la condición de una regla, su "antecedente" y a la acción de la regla, su "consecuente". Condiciones y acciones complejas permiten la representación de leyes matemáticas. La ley F = ma de Newton se convierte en Si x es fuerza e y es masa y z es aceleración, entonces, x = y veces z.
Los conceptos en PI son aún más complicados, ya que están representados mediante estructuras ricas semejantes a los marcos de Minsky (1975). Un marco representa una clase típica de objeto o situación (ver los tutoriales C y D por conocimientos básicos). Cada uno de los conceptos de PI incluye información sobre su lugar en una red jerárquica de conceptos: por ejemplo, los perros son clases de animales y tienen [17] collies y labradores como subclases, de modo que el concepto de perro tiene a animal como superordinado y a collie y labrador como subordinados. Además, los conceptos incluyen mensajes a los efectos de que puedan caer bajo el concepto diversos objetos. Lo más importante es que los conceptos van acompañados de reglas que describen propiedades generales. Lo que sigue es la representación del concepto de sonido que se usó en la simulación que realiza PI, del descubrimiento de la teoría ondulatoria del sonido:

[18]
Las condiciones, acciones, canal, estado, fiabilidad y
fuerza, las establece el programador. Las demás propiedades de la regla, desde
Emparejamientos-viejos hacia abajo, están inicialmente vacías, pero el
programa las va llenando a medida que se ejecuta. Por ejemplo, es muy importante
conocer los emparejamientos viejos (qué mensajes coincidieron previamente con
todas las condiciones e hicieron que la regla se activase) para evitar la
aplicación reiterada de la misma regla en una misma inferencia, impidiendo así
que se activen otras reglas. En los sistemas que se basan en reglas, esto se
llama "refracción". La pregunta Satisface-objetivo? se usó para
rastrear si la activación de una regla podría satisfacer los objetivos de un
problema, con el propósito de asegurar que esa regla se activará. El
Valor-actual se calcula cuando las condiciones de una regla se emparejan y
determina si tal regla será seleccionada como una de las que se activarán,
tomando en cuenta factores como su fuerza y su grado de activación. Las
Instancias-de-acción son las acciones de la regla con variables ligadas cuando
las condiciones se emparejan con los mensajes. El Apéndice 2 proporciona un
esbozo de las funciones de activación de reglas de LISP en PI.
Nótese que las reglas como Regla-3 no constituyen un análisis estricto o definición de "sonido". Expresan aquello que es propio de los sonidos, no aquello que es universalmente necesario y suficiente para que algo sea un sonido. Los diccionarios son de poca ayuda para formar estas definiciones, como lo muestra la siguiente entrada típica de diccionario (Guralnik, 1976, p. 1360):
sonido 1. a) vibraciones en el aire, agua, etc. que estimulan los nervios auditivos y producen la sensación de oír. b) la sensación auditiva producida por tales vibraciones.
En primer lugar, esta definición es altamente teórica, por cuanto se basa en el punto de vista científico de que los sonidos son vibraciones. En segundo lugar, resulta ser más bien circular, puesto que el diccionario define "auditivo" en términos de "oír" y "oír" en términos de percibir sonidos. Esta circularidad no es problema para dar cuenta del significado en informes como los que se discuten en el capítulo 4.
Las reglas generalmente especifican lo que es característico de objetos típicos y no lo que es universalmente cierto de ellos. Gracias a las críticas de Wittgenstein (1953) y Putnam (1975) en filosofía, Rosch (1973) en psicología y Minsky (1975) en IA, la noción tradicional del concepto como definido por condiciones necesarias y suficientes, se ha desacreditado. Wittgenstein señaló que no hay definiciones que capturen todas las instancias de conceptos complejos tales como "juego" y sólo esas. Es poco frecuente hallar estas definiciones fuera de la matemática. Los experimentos de Rosch y otros mostraron que los conceptos de la gente se organizan en torno a prototipos: un petirrojo, por ejemplo, es un pájaro más prototípico que un avestruz. Minsky [19] sostuvo que, para que haya una mayor flexibilidad computacional, los conceptos deberían representarse como marcos que describen casos típicos o idealizados. En conformidad con ello, las reglas proporcionan, en PI, una descripción aproximada de lo que es típico de los sonidos y no su definición. La noción tradicional de concepto como algo plenamente definido genera una interpretación engañosamente estricta de su significado, tema que será importante más adelante, en las discusiones acerca de cómo los conceptos se vuelven significativos (capítulo 4) y de la inconmensurabilidad de los esquemas conceptuales (capítulo 5).
¿Por qué PI usa mensajes, reglas y conceptos con tanta estructura? La justificación para complicar estas estructuras es, simplemente, que se puedan usar en procesos complejos: soportan un modelo de resolución de problemas e inferencia inductiva mucho más elaborado e interesante de lo que hubiera sido posible sin ellos. La cuestión de si un modelo computacional del pensamiento debe tener estructuras independientes que se correspondan con los conceptos, es un tema controvertido; las importantes arquitecturas cognitivas de Anderson (1983) y Laird, Rosenbloom y Newell (1986), no las tienen. Yo sostengo que constituyen una parte valiosa de una teoría de la cognición.
2.3.2. Resolución de Problemas
Resolución de problemas y activación expansiva de conceptos
La actividad central de PI es la resolución de problemas. Dado un conjunto de condiciones iniciales y de objetivos, activa reglas que conducirán desde las condiciones iniciales hasta los objetivos. Aquí está su simple representación del problema de explicar por qué el sonido se propaga y refleja:
La solución a este problema es una secuencia de activaciones de reglas que van en este caso, desde la suposición de que algún $x es una instancia arbitraria de sonido hasta la conclusión de que el sonido se refleja y se propaga. Una vez que el sistema tiene la teoría ondulatoria del sonido, la explicación puede consistir en una aplicación directa de las reglas según las cuales los sonidos son ondas y las ondas se propagan y reflejan. Sin embargo, la decisión sobre cuáles reglas activar, depende de muchas cuestiones no lógicas, tales como qué reglas están disponibles en la memoria, qué reglas son más fuertes, en el sentido de que tienen el mejor registro de éxitos, y qué reglas parecen más pertinentes a la situación concreta. (Para una exposición detallada de la operación de estos factores en los sistemas basados en reglas, ver Holland et al., 1986).
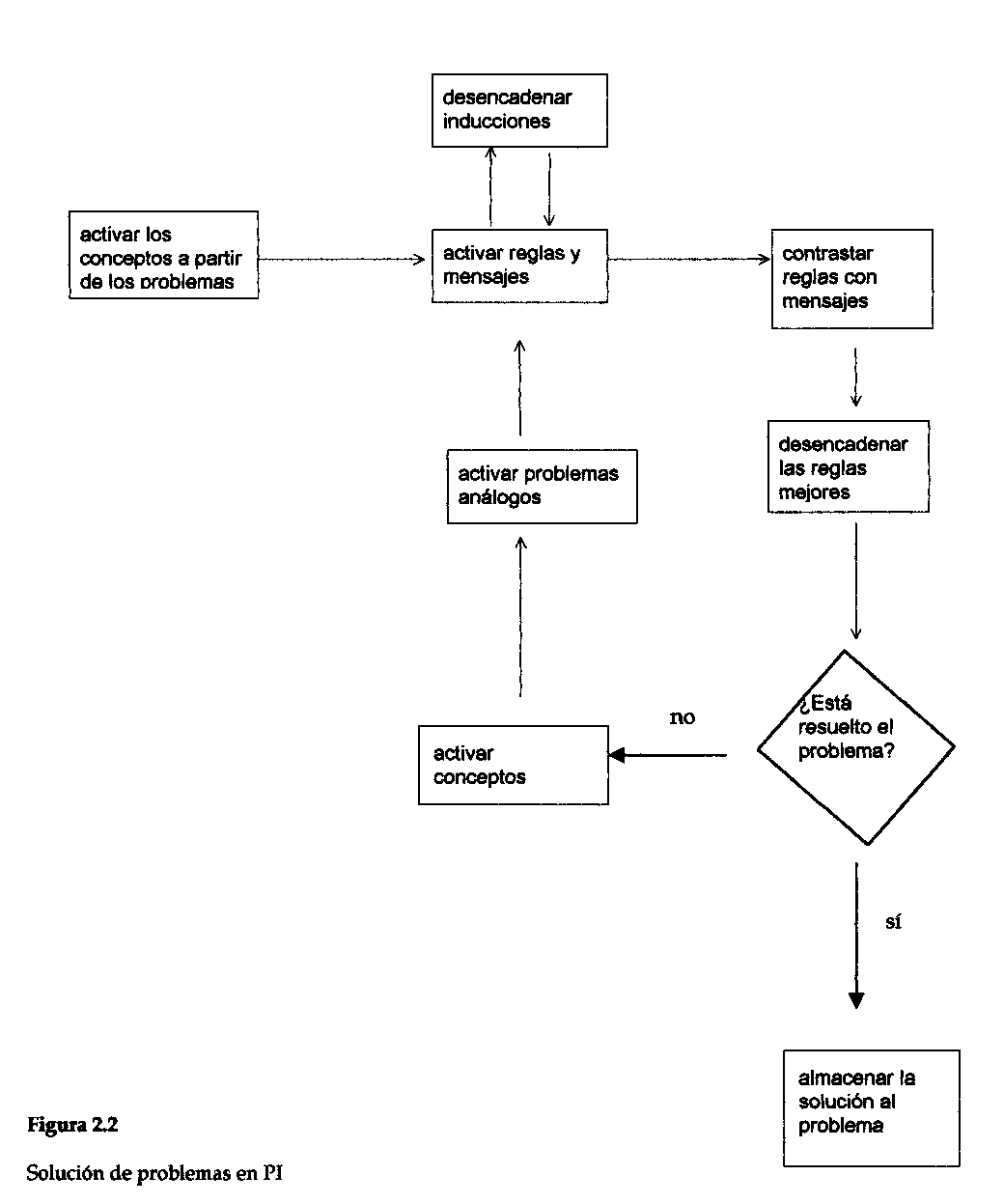
Cuando la gente resuelve problemas, sólo parte de la información más relevante está disponible en su memoria en un momento determinado cualquiera. PI modela la variación [20] en la accesibilidad a los elementos presentes en la memoria de un científico individual mediante un proceso de activación expansiva de conceptos y reglas. En cualquier momento dado, sólo se activa parte de la serie completa de conceptos y sólo se encuentran disponibles para activarse algunas reglas del total de ellas. Las reglas se asignan a los conceptos: como hemos visto, asignadas al concepto de sonido, hay reglas como aquella por la cual si x es un sonido e y es alguna persona que está cerca de x, entonces y oye x. Asignados al concepto de sonido, hay también mensajes que codifican hechos acerca de sonidos particulares, tal como aquel según el cual un sonido particular es bajo. PI compara todas las reglas de los conceptos activos con todos los mensajes de los conceptos activos; las reglas cuyas condiciones se emparejan se convierten así en candidatas a activarse. Puede activarse al mismo tiempo un número cualquiera de reglas, simulando procesamiento en paralelo. (El paralelismo es computacional y epistemológicamente importante; ver el capítulo 10). Cuando una regla se activa, se vuelven activos los conceptos que usa al funcionar. Así, si la regla "Si x es un perro, entonces x tiene pelo" se empareja con el mensaje "Lassie es un perro" y entonces se produce el nuevo mensaje "Lassie tiene pelo", siendo igualmente importante el hecho de que se activa el concepto de pelo. De este modo, en el próximo paso, se activarán nuevas series de mensajes y reglas sobre pelo. La activación puede propagarse hacia atrás, desde el objetivo hacia conceptos y reglas potencialmente útiles. Además, en la versión actual de PI (a diferencia de la versión descripta en Holland et al., 1986), la activación se propaga automáticamente hacia arriba y hacia abajo en la jerarquía de conceptos; por ejemplo, desde el sonido hacia arriba, hacia la sensación y el fenómeno superordinado y desde el sonido hacia abajo, hacia sus subordinados, como la música, la voz, el silbido, el disparo. El proceso de activación de las reglas y propagación de los conceptos continúa hasta haberse alcanzado los objetivos del problema. El proceso se esquematiza en la figura 2.2.
PI resuelve la cuestión de explicar la propagación y reflejo del sonido formando una teoría ondulatoria del sonido. Cómo fue exactamente lo que ocurrió cuando el pensador griego o romano descubrió por primera vez la teoría ondulatoria del sonido, no se sabe, pero algunos fragmentos de Crisipo (Sambursky, 1973) y Vitruvio (1960) sugieren que se había efectuado una asociación entre el sonido y las ondas acuáticas. PI ha simulado diversas maneras en que los conceptos de sonido y de onda pueden haberse vuelto simultáneamente activos; por ejemplo, a través de asociaciones que partiendo del sonido, van hacia, sucesivamente, la música, los instrumentos musicales, las cuerdas, las vibraciones de onda. La solución de PI para el problema de explicar por qué el sonido se propaga y se refleja pasa por activaciones de reglas y por la propagación de la activación, incluyendo la activación del concepto de onda que posibilita la formación de la hipótesis de que el sonido es una onda. En la figura 2.3 se presenta una cadena de asociaciones que van del sonido a la onda, simuladas en PI. Las activaciones de reglas están indicadas con flechas, y la propagación de la activación hacia subordinados y superordinados se indica mediante líneas verticales. En esta simulación, la activación se propaga del sonido hacia su subordinado, la música y otra vez hacia abajo, hacia los instrumentos musicales. Luego la regla según la cual la música instrumental se ejecuta con un instrumento se dispara y se activa el instrumento-de-cuerdas en cuanto subordinado de instrumento.
[21]
[22]
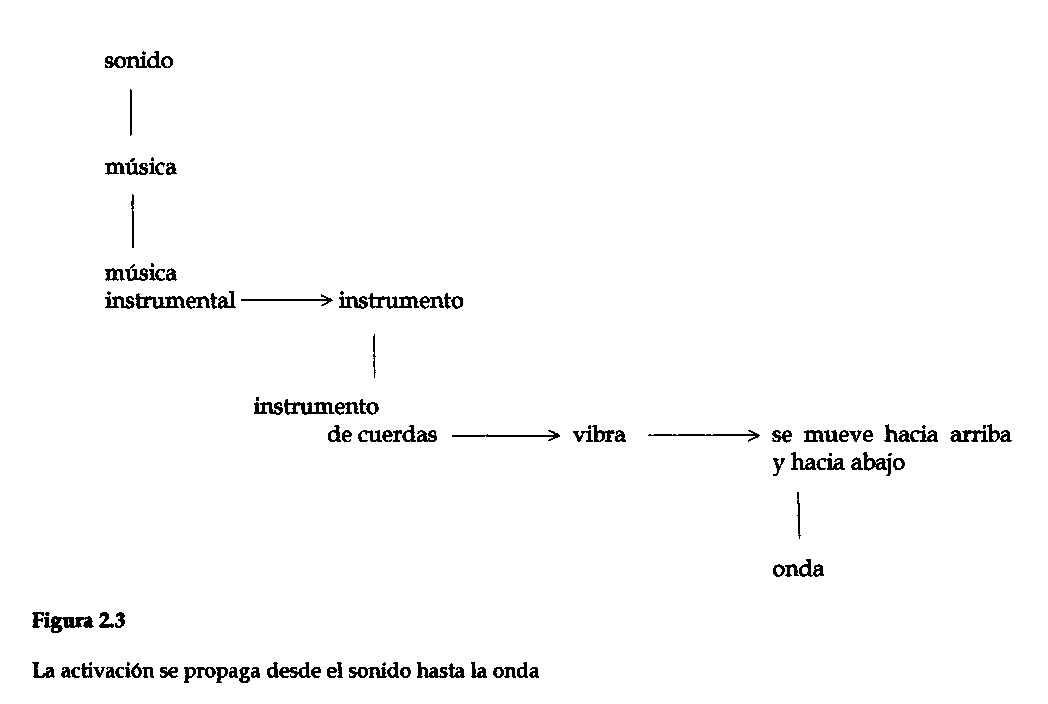
Se activan entonces dos reglas: los instrumentos de cuerdas vibran y lo que vibra se mueve de arriba abajo. Finalmente, la relación de que las ondas son una clase de movimiento de arriba abajo lleva a la activación del concepto de onda. Ver el Apéndice 3 para una descripción más completa de la ejecución de PI en este ejemplo. Obviamente, esta es sólo una de las muchas cadenas de asociaciones que pueden haber ocurrido cuando la teoría ondulatoria del sonido fue descubierta en la antigüedad por los griegos. En una simulación más realista ocurrirían muchas otras activaciones y desencadenamientos de reglas, simultáneamente con los que acaban de describirse. Pero de cualquier modo, la simulación da una idea de cómo podría producirse una asociación entre sonido y onda durante un intento por explicar por qué el sonido se propaga y se refleja.
Resolución Analógica de Problemas La resolución de problemas puede estar facilitada en gran medida por el uso de soluciones que en el pasado hayan tenido éxito. Keith Holyoak y yo hemos adaptado el mecanismo de propagación directa de PI de modo que proporcione un análisis de cómo pueden usarse las soluciones viejas para resolver problemas nuevos (Holyoak y Thagard, 1986). Las dos cuestiones claves en la resolución analógica de problemas son: 1) ¿Cómo se recuperan las soluciones exitosas pertinentes mientras se está resolviendo un problema? 2) ¿Cómo se saca partido de la analogía, una vez que se encontró una solución pertinente? En PI, las activaciones con propagación dirigidas ofrecen respuestas semejantes para estas dos preguntas.
Actualmente ejecutamos una simulación muy simplificada del problema de los rayos de Duncker (1945). El problema de los rayos consiste en resolver cómo usar una fuente de rayos para destruir un tumor en un paciente, teniendo en cuenta que una radiación a toda potencia destruiría el tejido entre la fuente y el tumor, llevando a la muerte del paciente. La gente tiene grandes dificultades para proponer una solución a este problema (Gick y Holyoak, 1980, 1983), pero su desempeño mejora mucho cuando se le da a conocer antes un problema análogo. El problema de la fortaleza consiste en tratar de resolver cómo puede un ejército [23] capturar una fortaleza, siendo imposible el ataque frontal con participación de todo el ejército. Una solución es dividir el ejército y usarlo para atacar la fortaleza desde diferentes puntos. Esta situación sugiere una solución análoga para el problema de los rayos, indicando una irradiación del tumor con rayos de menor intensidad desde diferentes direcciones.
Nuestra simulación actual modeliza la resolución analógica de problemas en los siguientes pasos. En primer lugar, debe resolverse el problema de base (aquí, el de la fortaleza) y su solución debe almacenarse mediante asociación con los conceptos mencionados en la descripción de tal problema. El problema de la fortaleza resuelto, por ejemplo, se representa mediante la siguiente estructura:
|
Nombre: |
capturar _ fortaleza |
|
Tipo-de-dato: |
problema |
|
Inicio: |
(ejército (obj_1) verdad) |
|
Objetivos: |
(capturar (obj_1 obj_2) verdad) |
|
Activación: |
1 |
|
Conceptos-asignados-a: |
(ejército fortaleza caminos entre capturar destruido) |
|
Reglas-usadas: |
regla_1_ejército, etc. |
|
Efectores: |
(dividir (obj_1) verdad) |
En segundo lugar, se intenta la solución para el problema central (aquí, el de los rayos). Ello inicia, en dos direcciones, la activación expansiva dirigida: hacia adelante, partiendo de los conceptos mencionados en las condiciones iniciales del problema central, mediante activación de reglas y, hacia atrás, partiendo de los conceptos mencionados en las condiciones fijadas para los objetivos. En tercer lugar, este proceso de activación de reglas lleva a la activación de conceptos a los que se les ha asignado el problema de la fortaleza. La figura 2.4 muestra un camino posible de activación usado por PI para simular. Aquí, una asociación que va desde rayo a disparar a bala a fusil a armas a luchar a conflicto a batalla a ejército, lleva a la activación del concepto ejército. Algunas de estas asociaciones se dan mediante la activación de reglas, como por ejemplo, que los rayos pueden disparar, mientras que otras se dan mediante relaciones subordinado/superordinado, por ejemplo, desde luchar a su superordinado, conflicto y hacia abajo, a otro subordinado, batalla. Gracias al paralelismo simulado por PI, una asociación del objetivo de destruir el tumor, lleva, al mismo tiempo, de destruir a vencer (ya que una manera de destruir algo es vencerlo) y luego, a conquistar y capturar. Dado que la solución almacenada del problema de la fortaleza está asignada a los conceptos recientemente activados de ejército y captura, esto acumula gradualmente la [24] activación. Cuando el grado de activación excede un umbral, PI desencadena un intento de explotar la analogía con mayor detalle.
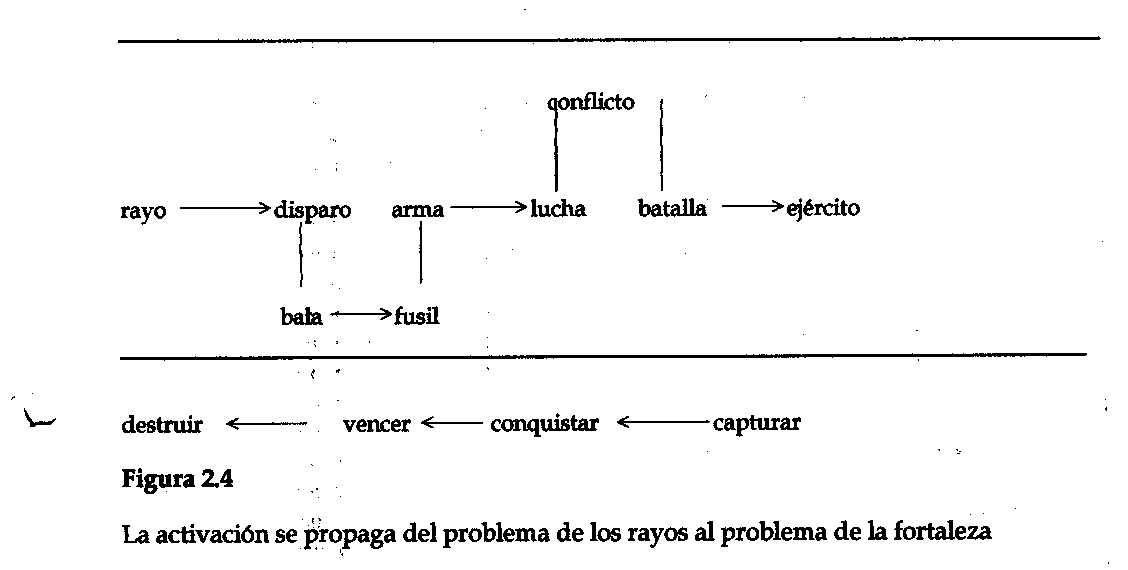
Para poder aprovechar una analogía es necesario haber notado las correspondencias entre las soluciones a los dos problemas y calcular cómo usar los pasos clave en la solución del primer problema para sugerir una solución al segundo. El cuarto paso, entonces, es realizar un diagrama de las soluciones a los dos problemas, que destaque los componentes análogos. PI obtiene este diagrama del registro de las activaciones expansivas, ya que en él figuran los conceptos que fueron responsables por la activación posterior de otros. Por lo tanto, puede rastrear hacia atrás desde ejército, para determinar que fue activado por rayo, y establecer que la fuente de los rayos en el problema de los rayos y el ejército en el problema de la fortaleza, son análogos. Por supuesto que el camino de la activación hacia ejército incluía además otros conceptos, pero rayo es el único concepto que fue activado como parte de la descripción del problema objetivo.
El establecimiento de los componentes análogos posibilita el quinto paso, en el que se realizan acciones análogas dentro del problema objetivo. PI almacena, junto con una solución al problema, una lista de "efectores", las acciones proyectadas para actuar y que llevaron a la solución del problema. En el problema de la fortaleza, los efectores fueron la división del ejército y el desplazamiento independiente de las divisiones hacia la fortaleza. Usando el diagrama ya establecido, PI determina que podría hallarse una solución al problema de los rayos alcanzando los dos sub-objetivos de dividir el rayo y desplazar sus componentes de manera separada hacia el objetivo. En este punto, se reanuda el intento de resolver el problema del rayo mediante los procesos estándar de desencadenamiento-de-reglas y activación expansiva. Ahora, los nuevos sub-objetivos proporcionan una descomposición del problema del rayo, erróneamente estructurado [25] antes. La analogía con el problema de la fortaleza no brinda una solución completa al problema del rayo, pero permite sugerir los pasos clave de la solución.
Después que PI resuelve un problema analógicamente, produciendo una solución mediante el uso de otra previa, construye un esquema analógico, que constituye una abstracción de esas dos soluciones anteriores (ver el tutorial D para una introducción a la noción psicológica de esquema). Dado que el problema de la fortaleza ha contribuido a solucionar el problema del rayo, PI examina cómo están enunciados los dos problemas, para ver qué tienen en común. Trata de obtener una versión abstracta de los dos problemas, usando las reglas almacenadas con los conceptos de los correspondientes problemas. En los problemas de la fortaleza y del rayo, hay suficiente semejanza como para producir la siguiente estructura:
|
Nombre: |
capturar-fortaleza/destruir-tumor |
|
Tipo-de-dato: |
esquema de problema |
|
Inicio: |
(fuerzas
($x) verdad) |
|
Meta: |
(vencer ($x $y) verdad) |
|
Efectores: |
(dividir ($x) verdad) |
Luego se asocia esta estructura con los conceptos pertinentes, tales como fuerzas, y queda disponible para futuras resoluciones de problemas analógicas. Puede resultar mucho más conveniente usar este esquema que los dos problemas de los que está formado, puesto que será más fácil diagramar un nuevo problema concreto para esta abstracción que para los problemas de la fortaleza o del rayo. Cualquier nuevo problema cuyos conceptos activen suficientemente los de fuerzas, objetivo y vencer, será capaz de aprovechar la posible solución de dividir las fuerzas.
Los procesos descriptos simulan muchos de los resultados experimentales de Duncker (1945) y de Gick y Holyoak (1980, 1983). Holyoak y Thagard describen cómo tal modelo puede dar cuenta de resultados experimentales como la eficacia de la intuición en la resolución de problemas, la eficacia de los esquemas de problemas y el hecho de que las similitudes estructurales (que cumplen un papel causal en la determinación de las soluciones) son más importantes que las similitudes superficiales en la transferencia analógica.
Procesos extralógicos Un lógico naturalmente preguntará, ¿por qué preocuparse de toda esta activación expansiva? ¿Por qué no tomar las consecuencias lógicas de las creencias actuales y agregarlas simplemente a la serie de creencias? Ya hemos visto que ninguna memoria finita podría manejar tal procedimiento. Un sistema no debe trastornar una memoria finita con hechos inútiles. Sin embargo, aún se podría decir que sería más elegante considerar, en cada paso, todos los mensajes y reglas almacenados en la memoria. El problema computacional respecto de esta sugerencia es, simplemente, que hay demasiados en un sistema tan grande como el de un ser [26] humano. Lo que aparece como limitaciones en la memoria humana (nuestra incapacidad de pensar en todas las cuestiones pertinentes en un tiempo dado) puede ser, de hecho, importante para el pensamiento, puesto que no seríamos capaces de extraer ninguna conclusión si estuviésemos abrumados de información. Un sistema de resolución de problemas debe tener la capacidad de enfocar la atención sobre las inferencias que la experiencia señale que pueden brindar prometedoras vías de solución. El mecanismo de activación propagada en PI está destinado a mostrar cómo la resolución de problemas puede enfocarse a partir de las reglas pertinentes y las analogías prometedoras.
Debería estar claro ahora por qué los conceptos tienen que ser tan complejos. En PI, los conceptos cumplen el papel crucial de propagar la activación, de determinar qué información está disponible en todo momento, y se vuelven activos o cesan de activarse declinando cuando ya no se los usa. Organizan conjuntamente diversos mensajes y reglas. Su papel en la resolución analógica de problemas es central, tanto por su capacidad de hallar analogías útiles mediante la activación expansiva, como por aprovecharlas usando los rastros de activaciones.
En el capítulo 3, propongo que no podemos comprender las teorías y las explicaciones en la ciencia sin tener en cuenta qué clase de procesos complejos de resolución de problemas y de aprendizaje esta usando PI para el estudio. Si ello es correcto, entonces los análisis computacionales dados más arriba son de un interés más que psicológico, ya que serían igualmente esenciales para la comprensión filosófica del conocimiento científico.
De este modo, PI necesita estructuras de datos complejas para ser capaz de realizar procesos que controlen efectivamente la solución de problemas y la inducción. Contrapóngase esto a la programación lógica, usando el lenguaje Prolog (Clocksin y Mellish, 1981). Prolog es útil para muchas aplicaciones por su sintaxis semejante a la lógica y su mecanismo de deducción. Las expresiones en Prolog son semejantes a las del cálculo de predicados, aunque deban también entenderse como instrucciones de programación. Por ejemplo, el enunciado "Todo cobre conduce electricidad" se representa en Prolog como conduce-electricidad (x) ← cobre (x). En cuanto procedimiento, esto se interpreta como Si usted quiere mostrar que algo conduce electricidad, primero muestre que es cobre. Por ejemplo, si la base de datos contuvo el enunciado cobre(espécimen47) y se pregunta al sistema si conduce-electricidad(espécimen47), usará la regla anterior para deducir que, en verdad, el espécimen 47, conduce electricidad. La deducción se hace mediante un probador de resolución de teoremas: Prolog compara las negaciones de la expresión que ha de ser probada con la serie de expresiones ya afirmadas y trata de obtener una contradicción. Si obtiene una contradicción, entonces la afirmación en cuestión se considera probada y se la añade a la base de datos.
Es más fácil escribir programas que razonen en Prolog que en LISP porque el mecanismo de inferencia ya está en su lugar. Se puede, por supuesto, escribir un probador de resolución de teoremas, en LISP o en cualquier otro lenguaje de programación, pero Prolog tiene la ventaja de proveer al programador de un mecanismo de inferencia desde el primer momento. Sin embargo, la ventaja, cuando se trata de producir modelos cognitivos de los [27] que necesita la filosofía computacional de la ciencia, es ilusoria. Feigenbaum and McCorduck (1983, p. 122) sostienen que "los éxitos más importantes de la IA se deben a su dominio de los métodos mediante los cuales se puede usar el conocimiento para controlar la búsqueda de soluciones a problemas complejos. Lo último que un ingeniero del conocimiento desearía hacer es traspasar el control a un proceso ‘automático’ de prueba de teoremas que conduce búsquedas masivas sin que el conocimiento ejerza, en la base de conocimientos, el seguimiento de cada uno de los pasos. Tales búsquedas descontroladas pueden ser extremadamente consumidoras de tiempo." PI usa estructuras de datos complejas, como conceptos y reglas, para darles a sus procedimientos de resolución de problemas e inducción un control mayor del que podría tener un simple sistema deductivo.
Desde luego que, dado que Prolog es un lenguaje de programación completo, al igual que un mecanismo deductivo, puede usarse para producir estructuras de datos y procesos muy parecidos a los que PI emplea en LISP. En este punto, sin embargo, se termina cualquier semejanza entre Prolog y la lógica, y su mecanismo deductivo de prueba de teoremas deja de cumplir un papel serio en el modelo cognitivo que se está desarrollando.
La justificación dada hasta ahora para el mecanismo de activación expansiva del PI, es tanto psicológica, porque imita en alguna medida el acceso a la memoria humana (ver Holland et al., 1986, cap. 2), como computacional, porque es necesario acotar y enfocar la resolución de problemas. Un argumento computacional aún más fuerte surge de la naturaleza de la inducción. La activación restringida de los conceptos, reglas y mensajes resulta decisiva para orientar y encuadrar la realización de inferencias inductivas.
2.3.3. Inducción
He tratado de demostrar antes la necesidad de restringir la deducción para poder controlar qué inferencias deductivas se obtienen, y cuándo. Las restricciones son aún más esenciales para la inferencia inductiva, es decir, la inferencia que lleve a conclusiones que no se siguen necesariamente de lo que ya se conoce. La inducción es por naturaleza más riesgosa que la deducción, puesto que puede llevar a conclusiones que no sólo son inútiles sino, además, falsas. Al menos en la deducción, lo que se sigue de premisas verdaderas, debe ser verdadero, mientras que la inducción implica de manera inevitable algún tipo de variación. Aunque el lector pueda haber observado numerosas instancias de conducción de electricidad por el cobre; generalizar que todo cobre conduce electricidad introduce, a pesar de todo, incertidumbre.
Puede parecer menos que óptimo diseñar un sistema que restrinja la atención a sólo una fracción de la información almacenada en la memoria. En discusiones sobre inducción, filósofos como Carnap (1950) y Harman (1973) han abogado por condiciones de evidencia total, según las cuales las inferencias inductivas de uno deberían tomar en cuenta toda la evidencia pertinente a la conclusión. Tal exigencia es, impracticable computacionalmente, puesto que requeriría una búsqueda comprehensiva en toda la información almacenada. Necesitamos medios más prácticos para concentrarnos en la información pertinente a los fines de nuestros propósitos.
[28]
Además, al hacer inducciones, no queremos solamente alcanzar conclusiones bien garantizadas: queremos también producir reglas que serán útiles para su uso futuro en la resolución de problemas y en la explicación. Por ejemplo, puedo inducir que todas las tejas del techo de mi casa tienen entre 1.000 y 2.000 manchitas, pero ¿por qué molestarse en contarlas? Del mismo modo, es poco probable que el lector dedique mucho tiempo a generalizar sobre el número de líneas o palabras que hay en cada página de este libro. La inducción debe tomar en cuenta los objetivos del sistema. (Ver Holland et al., 1986, cap. 1, para una exposición más completa de la pragmática de la inducción; compárese con la discusión de la importancia de los intereses en el razonamiento, en Harman, 1986.)
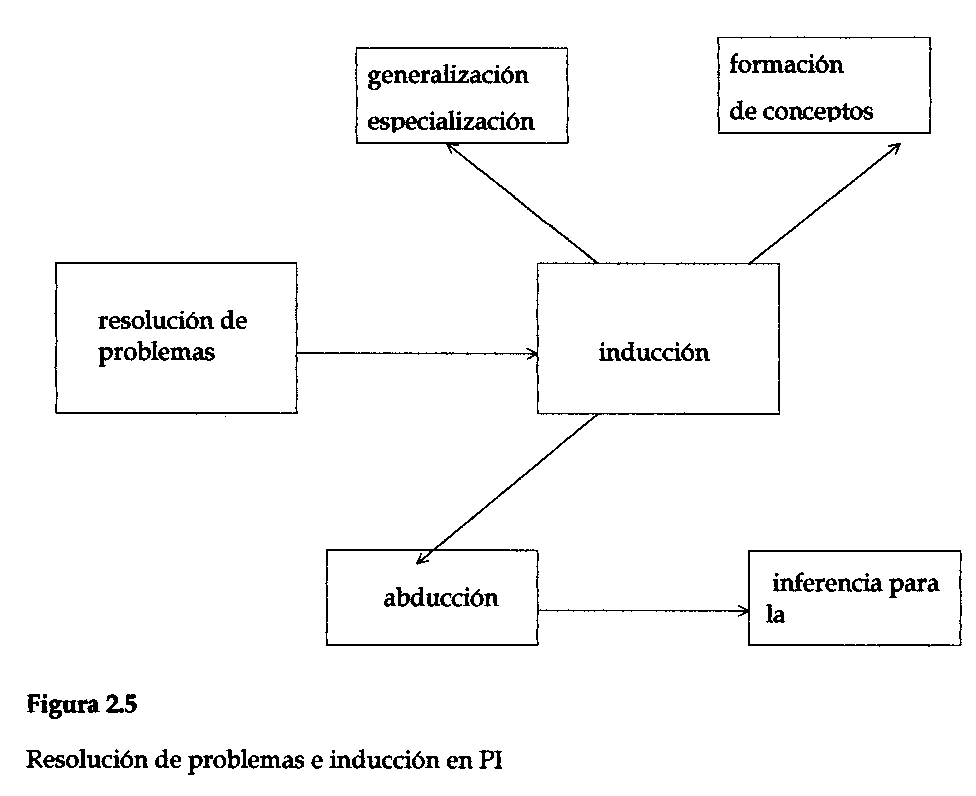
Así, PI sólo realiza inducción en el contexto de la resolución de problemas. En cada paso de un intento de solución a un problema, PI monitorea la lista de los mensajes, reglas y conceptos, que esté activa en ese momento. De esta manera, no se realizará ninguna inferencia inductiva que no sea pertinente a la situación vinculada con la resolución del problema en curso. PI desencadena intentos en varias clases de inferencia inductiva, incluyendo por lo común generalización, abducción y formación de conceptos; ver la figura 2.5, que completa la figura 2.2.
Trataré la generalización muy brevemente, ya que se discute con mayor extensión en otro trabajo (Holland et al., 1986, cap. 8). Si la lista de mensajes activos de PI incluye la información de que algunos objetos caen bajo dos conceptos, entonces se realiza el intento de ver si esto se aplica generalmente. Por ejemplo, los mensajes (cobre (espécimen14) verdad 1) y (conduce_electricidad (espécimen14) verdad 1) desencadenarán intentos de generalizar que todo lo que es cobre conduce electricidad y que todo lo que conduce electricidad es cobre. Se utiliza luego más información almacenada con los conceptos de cobre y conduce_electricidad para determinar si alguna de estas generalizaciones está garantizada. El [29] intento de generalizar se interrumpirá pronto si un control de los conceptos pertinentes determina que hay ejemplos en contra de la posible generalización o que la generalización ya se había realizado. De otro modo, PI considera si hay suficiente evidencia para garantizar la generalización, tomando en cuenta tanto la cantidad de instancias en común como el conocimiento de base sobre la variabilidad de las clases de cosas en cuestión. La variabilidad es importante en la determinación de cuántas instancias se requieren para que se satisfagan las condiciones que permiten considerar aceptable una generalización. Por ejemplo, el lector estaría más dispuesto a generalizar a partir de unas pocas instancias que el metal conduce electricidad, que a generalizar que una nueva clase de pájaro tiene un color determinado, porque los pájaros varían más en cuanto a su color, que los metales en cuanto a sus propiedades eléctricas.
La generalización en PI tiene mucho en común con la teoría tradicional de la confirmación, que analiza cómo pueden confirmarse las leyes a partir de los casos (Hempel, 1965), pero también hay importantes diferencias. En primer lugar, PI no trata la confirmación de las leyes aisladamente, sino que ve a la generalización como algo que se desencadena durante la actividad científica de la resolución de problemas; esto añade un componente pragmático, dirigido a objetivos determinados, que contribuye a evitar las famosas paradojas de la teoría de la confirmación (Holland et al., capítulo 8). En segundo lugar, PI no trata solamente los casos que confirman las leyes, sino también el conocimiento de base sobre la variabilida. Esto requiere usar la información almacenada en conceptos relativos a las relaciones de superordinación y subordinación. Por ejemplo, para poder generalizar que los cuervos son negros, es necesario saber que los cuervos son una clase de pájaro y que el negro es una clase de color y qué otras clases de pájaros y de colores hay (el algoritmo que usa PI está esquematizado en el apéndice 2). De este modo, los recursos de resolución de problemas y representación del conocimiento de PI van mucho más allá de lo que puede hacerse en la teoría clásica de la confirmación.
Otras clases de aprendizaje (formación de conceptos y abducción) se discutirán en capítulos subsiguientes. El capítulo 4 describe el papel de la abducción en la formación de hipótesis y la importancia de la formación de los conceptos mediante la combinación conceptual para la creación de conceptos teóricos. El punto fundamental para tener en mente aquí es que PI nunca pierde tiempo tratando de formar todas las hipótesis posibles o todos los conceptos posibles. La abducción y la combinación conceptual se desencadenan sólo cuando están activos los conceptos y las reglas pertinentes. La concentración en lo que es pertinente e importante se logra mediante el control de la propagación de la activación a través del proceso de resolución de problemas.
2.3.4. Las limitaciones de PI
PI tiene muchos rasgos convenientes para un modelo de los procesos cognitivos de los científicos, pero también tiene claras limitaciones. Las simulaciones ejecutadas hasta ahora han sido pequeñas, no habiendo usado ninguna más de 60 reglas o conceptos, de modo que sólo captura una reducida parte del conocimiento del dominio: ver el apéndice 3, para un [30] ejemplo. Un test más fuerte del modelo requerirá simulaciones que implican formalizar grandes cantidades de conocimiento del dominio, sin preselección de conceptos y reglas que aseguren los caminos de la solución deseada. Las soluciones a los problemas en curso no emplean virtualmente conocimientos sobre el espacio, el tiempo y la causalidad, los cuales son importantes para la resolución de problemas y la explicación (ver la sección 3.5.2). Algunos mecanismos que emplea PI, tales como su particular clase de activación propagada mediante la activación de reglas y las relaciones superordinado/subordinado, tienen que ser ya testeados por experimentos psicológicos. Su mecanismo de generalización sólo es capaz de inferir leyes cualitativas muy simples, puesto que carece de los mecanismos heurísticos para formar leyes matemáticas que están presentes en el programa BACON (Langley et al., 1987) y la capacidad de usar el conocimiento relativo a un dominio para orientar la búsqueda de reglas que tiene el programa Meta-DENDRAL (Buchanan y Mitchell, 1978). La implementación de la resolución analógica de problemas que realiza PI también necesita mejoramiento; se ha desarrollado un método muy superior de proyección de una analogía en otra, pero aún no se lo ha integrado con PI (Holyoak y Thagard, 1987). Más limitaciones de PI relativas al descubrimiento y a la justificación de hipótesis se indicarán en los capítulos 4 y 5. No obstante, PI ofrece un esquema computacional inicial para investigar las cuestiones vinculadas con el conocimiento científico.
2.4. Equivalencia expresiva y de procedimiento
Pese a los argumentos anteriores relativos a la importancia de conceptos en la representación del conocimiento, quizá haya algunos escépticos que quieran sostener su carácter de prescindible sobre la base general de que su contenido puede traducirse a estructuras más simples. A mediados de los ‘70, hubo una bulliciosa actividad en IA, que empleaba la ambigua pero sugerente noción de marco, de Minsky. Hayes (1979) señaló que hay una traducción natural de las representaciones de marcos al cálculo de predicados: se puede transformar un marco en una conjunción de oraciones en el cálculo de predicados, en la cual cada oración representa la información en una ranura del marco. De este modo, toda la información de las reglas y conceptos de PI podría traducirse en oraciones del cálculo de predicados.
Sin embargo, la existencia de tal traducción de ninguna manera disminuye la importancia de contar con representaciones ricas de reglas y conceptos. Comparemos dos sistemas de numeración: los números arábigos 1, 2, 3 y los números romanos, I, II, III. Si a los números romanos se añade el cómodo número 0, entonces hay una evidente traducción de números arábigos a números romanos, de modo que podría decirse que no hay entre estos dos sistemas una diferencia interesante. Pero consideremos nuestros algoritmos para realizar multiplicaciones y divisiones grandes. A una edad temprana aprendemos cómo dividir, [31] digamos 598 por 46, a lo largo de estas líneas: 46 en 59 está una vez, con un resto de 13 y 46 está en 138 3 veces, de manera que la respuesta es 13. Comparemos con el intento de dividir DXCVIII por XLIV. La representación romana no se presta tan fácilmente a un algoritmo simple para realizar una división grande. De este modo, aunque podamos decir que los números romanos y arábigos son expresivamente equivalentes porque pueden traducirse el uno al otro y así tienen el mismo contenido, sería un error decir que son equivalentes en cuanto al procedimiento, puesto que no son apropiados para todos los procedimientos.
La sola distinción entre equivalencia expresiva y equivalencia de procedimiento, tiene muchas aplicaciones. Dada la equivalencia expresiva entre dos sistemas y un procedimiento en uno de ellos, siempre podemos encontrar un procedimiento correspondiente en el otro. Pero el procedimiento hallado puede ser muy ineficiente. Para el caso de los números romanos, podemos traducirlos simplemente a números arábigos, usar nuestros algoritmos familiares con ellos y luego volverlos a traducir, en lugar de intentar la obtención de un algoritmo para la división grande, directamente. Es evidente, sin embargo, que este proceso toma mucho tiempo extra, de manera que no constituye una ventaja frente al uso de los números arábigos. De manera similar, los procedimientos en los sistemas de marcos pueden ser más eficientes para clases particulares de inferencias que los hallados en sistemas lógicos menos especializados. Cualquier computadora digital es computacionalmente equivalente a una máquina de Turing, la cual es un dispositivo extremadamente simple consistente sólo en una cinta con recuadros y una cabeza que puede escribir ceros y unos en los recuadros. Pero este hecho no es de mucho interés para comprender la inteligencia, ya que las máquinas de Turing son lentas y penosas de programar. El diseño de sistemas inteligentes, por selección natural o por ingenieros humanos, tiene en cuenta, inevitablemente, la velocidad de las operaciones. De aquí la gran importancia que tiene para comprender la naturaleza de la mente, la actual oleada de investigaciones sobre cómo las arquitecturas paralelas para computadoras pueden acelerar el procesamiento (véase el capítulo 10 y Thagard, 1986).
La distinción entre la equivalencia expresiva y la equivalencia de procedimiento es importante también para la psicología teórica. Hubo entusiastas debates en torno de si la mente emplea imágenes mentales además de proposiciones y si emplea grandes estructuras llamadas "esquemas" además de proposiciones más simples (véase tutorial D). Algunos teóricos han argumentado que, dado que el contenido de toda imagen o esquema puede traducirse a proposiciones, no hay necesidad de proponer las estructuras adicionales. Pero las imágenes y los esquemas podrían tener procedimientos asociados con ellos, que serían mucho más difíciles de realizar en un sistema puramente proposicional; las imágenes, por ejemplo, se pueden hacer rotar o pueden manipularse de modo sistemático. Así, usando factores tales como la velocidad de procesamiento y diferencias cualitativas, puede encontrarse evidencia empírica que sostenga la existencia en el pensamiento humano, de estructuras más complejas que las halladas en las reglas y conceptos de PI.
[32]
2.5. ResumenUna comprensión del conocimiento científico requerirá la representación de las observaciones,
leyes, teorías, conceptos y soluciones a problemas. Para producir una descripción completa de los roles que estos elementos cumplen en actividades tales como la resolución de problemas y el descubrimiento, es necesario usar representaciones con más estructura de la que admitiría un modelo lógico. Los conceptos de PI requieren mucha estructura interna a causa de la forma en que agrupan la información y propagan la activación por el sistema durante la resolución de los problemas. La equivalencia expresiva de dos sistemas no implica la equivalencia de procedimiento, y las cuestiones de procedimiento son centrales a la comprensión del desarrollo y aplicación del conocimiento científico.
[33]
Capítulo 3Teorías y explicaciones
Las teorías científicas son nuestros logros epistémicos más importantes. Nuestro conocimiento de los aspectos individuales de la información es poco comparado con teorías tales como la teoría general de la relatividad y la teoría de la evolución por selección natural, que configuran nuestra comprensión de muchas clases diferentes de fenómenos. Podríamos inclinarnos a pensar que el conocimiento común (ver) cambia y se desarrolla meramente mediante añadidos y supresiones de fragmentos de información; sin embargo, el cambio teórico exige alteraciones globales mucho más complejas. Pero, ¿qué son estas entidades que constituyen la parte más impresionante de nuestro conocimiento?
Los investigadores en filosofía de la ciencia de los últimos cincuenta años han usado tres clases de aproximaciones al problema de la naturaleza de las teorías cientIficas. Siguiendo la clasificación semiótica tradicional del capítulo 2, llamaré a estos enfoques, sintáctico, semántico y pragmático. Los positivistas lógicos consideraron las teorías científicas como estructuras sintácticas -series de oraciones, con una formalización axiomática ideal en un sistema lógico (Hempel, 1965, pp. 182-183). En la década pasada, una concepción semántica (de teoría de conjuntos) (ver) de las teorías se fue volviendo cada vez más popular; esta concepción abstrae de formulaciones sintácticas particulares de teorías y las interpreta en términos de conjuntos de modelos, en el sentido tarskiano explicado en el tutorial B (revisar). Otra tendencia reciente, difundida entre filósofos con una inclinación más histórica, ha sido pragmática porque considera a las teorías como dispositivos usados por los científicos en contextos particulares (revisar). Entre los filósofos que construyen teorías pragmáticamente, están Kuhn (1970b), quien enfatiza el rol de los paradigmas en las comunidades históricas, y Laudan (1977), quien subraya el papel de las teorías en la resolución de problemas empíricos y conceptuales.
Las próximas secciones describen algunas de las fortalezas y debilidades de estos tres enfoques. Sostendré que un testimonio plenamente adecuado de las teorías científicas, debe ser pragmático: la concentración formalista sobre los sólos rasgos sintácticos o semánticos de las teorías, descuida inevitablemente algunos de sus aspectos esenciales. Sin embargo, los testimonios pragmáticos de orientación histórica de Kuhn y otros, han fracasado en el desarrollo de análisis filosóficos adecuados porque han sido incapaces de añadir suficiente contenido a nociones [34]ambiguas como paradigmas y soluciones de problemas. Usando ideas computacionales, puede desarrollarse un testimonio pragmático más poderoso. Voy a construir una teoría en cuanto complejo de estructuras de datos de la clase descripta en el capítulo anterior y voy a plantear que el resultado es práctica, histórica, y filosóficamente superior a los enfoques sintácticos y semánticos.
3.1. Requisitos para una exposición de la naturaleza de las teorías
¿Qué debemos pedirle a un testimonio sobre la naturaleza de las teorías científicas? Pienso que ha de ser adecuado en tres niveles distintos pero relacionados: el práctico, el histórico y el filosófico. Queremos un testimonio que 1) sirva para describir la práctica cotidiana de los científicos en cuanto a su uso de las teorías, 2) organize los modos en que las teorías están desarrolladas históricamente, 3) de lugar a tratamientos filosóficamente satisfactorios de temas tan importantes en la filosofía de la ciencia como la naturaleza de la explicación.
Un testimonio que sea prácticamente adecuado, debe mostrar cómo pueden funcionar las teorías en las distintas maneras en que las usan los científicos en la explicación, la resolución de problemas, el desarrollo de conceptos, etc. El uso en estas operaciones intelectuales supone que una teoría debe ser una entidad psicológicamente real, capaz de funcionar en las operaciones cognitivas de los científicos. Tal funcionamiento no es una cuestión puramente individual, porque una teoría debe tener la capacidad de que los miembros de una comunidad científica la compartan y que los nuevos miembros de esa comunidad, la aprendan. Si la filosofía de la ciencia ha de ser filosofía de la ciencia más que epistemología abstracta, entonces tendrá que relacionarse con la psicología puesto que su testimonio de la estructura del conocimiento científico da cuenta de la manera en que se estructura el conocimiento en las mentes individuales. La adecuación práctica exige que un testimonio sea suficientemente amplio como para poder caracterizar los usos, tanto de las teorías matemáticas como por ejemplo, la mecánica de Newton, como las que son primordialmente cualitativas, tal como la teoría de la evolución de Darwin.
Un testimonio históricamente adecuado debe poder describir cómo se desarrollan las teorías en el tiempo, de un modo fiel a la historia de la ciencia. Ha de ser suficientemente flexible para poder dar cuenta de cómo se descubrieron las teorías y cómo han pasado por el cambio de sus conceptos, a la vez que de elucidar la noción de identidad de teorías. El testimonio también debe ser capaz de describir las relaciones dinámicas entre las teorías, tal como la reducción o el reemplazo de una teoría por otra y la rivalidad de las explicaciones en teorías del mismo dominio.
Un testimonio de la naturaleza de las teorías científicas, filosóficamente adecuado, debe contribuir con soluciones plausibles y rigurosas a otros problemas centrales en la filosofía de la ciencia. En principio, un testimonio debe sugerir un análisis de la naturaleza de la explicación científica. Luego, estrechamente vinculado a lo anterior, necesitamos un tratamiento detallado de los problemas científicos y de sus soluciones. Debemos tener la capacidad de mostrar cómo la teoría puede emplearse de manera realista, en cuanto sustancialmente verdadera, pero también, cómo puede construirse instrumentalmente, en cuanto [35] dispositivo útil para la predicción y otras operaciones.
Debemos ser capaces también, de dar un testimonio acerca de cómo se confirma y justifica una teoría más aceptable que otras rivales. Finalmente, un testimonio acerca de la naturaleza de las teorías debería sugerir una respuesta a la difícil cuestión del significado de los términos teóricos.
3.2. Crítica de los testimonios predominantes
Para comenzar la exposición de que un testimonio computacional puede ser más adecuado prácticamente, históricamente y filosóficamente, que sus alternativas, pasemos revista brevemente a los defectos de los testimonios positivista, de la teoría de conjuntos y kuhniano.
3.2.1. El testimonio positivista sintáctico
Considérese primero la doctrina de los positivistas lógicos según la cual una teoría es un conjunto axiomático de oraciones. Muchos críticos han señalado que este enfoque tiene poco que ver con el modo en que se usa la mayoría de las teorías científicas. Las axiomatizaciones rigurosas son pocas en la ciencia y deberíamos ser escépticos sobre el mantenimiento en cuanto ideal, de algo que se concreta tan raramente. Más aún, la utilidad del logro de una axiomatización completa es dudosa, ya que los sistemas de axiomas son herramientas complicadas para realizar con ellas las tareas de resolución de problemas y explicación. Por supuesto que la formalización de algún tipo será necesaria para cualquier implementación computacional del conocimiento científico, pero tendrá que estar dirigida hacia cuestiones de procedimiento, más que al rigor lógico. El énfasis en la sintaxis propio de la visión de las teorías como sistemas de axiomas lleva a descuidar consideraciones semánticas importantes para la comprensión del desarrollo de los conceptos y a descuidar consideraciones pragmáticas cruciales para la justificación y la explicación. Los sistemas de axiomas podrían verse como psicológicamente reales en caso de centrarnos en los científicos resolviendo problemas directamente mediante deducciones de una serie de proposiciones, pero ya hemos visto en el último capítulo la necesidad de una aproximación mucho más rica. En suma, el testimonio positivista no es prácticamente adecuado.
Las críticas más influyentes al testimonio positivista han venido de historiadores y de filósofos con orientación histórica (Kuhn, 1970b; Toulmin, 1953; Hanson, 1958). El reproche que realizan a los positivistas lógicos es haber descuidado la dramática extensión del cambio conceptual en la historia de la ciencia, un descuido que radica, en parte, en el supuesto de que el significado de los términos teóricos deriva de la interpretación parcial a partir de los resultados de la observación. Para mencionar un ejemplo, Kuhn (1970b, p.101ss) dice que el reemplazo de la mecánica newtoniana por la teoría de la relatividad de Einstein no encaja en el modelo preciso de reducción consistente en deducir una serie de oraciones de otra. La dinámica de las teorías no está bien representada [35] en el testimonio positivista. El descubrimiento se excluyó explícitamente como tema en la filosofía de la ciencia de los positivistas tales como Reichenbach (1938), quien distinguió entre el contexto de descubrimiento y el de justificación. Como veremos en los capítulos 4 y 5, un enfoque computacional puede dar un testimonio integrado del descubrimiento y la justificación.
La pertinencia filosófica del testimonio positivista ha sido cuestionada por críticas sustentadas por los enfoques relacionados de la explicación y la confirmación. El modelo de explicación nomológico - deductivo, que construye una explicación como deducción a partir de una serie de oraciones que incluyen leyes, ha sido criticado por su fracaso en ofrecer condiciones suficientes o necesarias para la explicación (véase el tutorial A para un resumen del modelo nomológico-deductivo). La teoría de la confirmación ha zozobrado en las intratables paradojas de Goodman (1965) y Hempel (1965), a las que se ha dado una desenlace pragmático en otro trabajo (Holland et al., 1986, cap. 8) . En el capítulo 5 sostengo que la justificación de las teorías científicas está mejor representada por un modelo de inferencia para la mejor explicación, que por el modelo hipotético-deductivo de confirmación y muestro lo bien que el testimonio computacional de las teorías engrana con la inferencia hacia la mejor explicación. Otro importante problema con el testimonio positivista se vincula con el significado de los términos teóricos. Se lo ha puesto en tela de juicio en relación con la viabilidad de la noción de interpretación parcial y, aún con más fundamento, respecto de si es defendible la distinción entre términos teóricos y términos observacionales. En el capítulo 4 se presentará la cuestión del significado de los términos teóricos.
3.2.2. El paradigma de Kuhn
La noción de paradigma de T. S. Kuhn ha reemplazado el testimonio positivista de las teorías en muchas discusiones, particularmente en las ciencias sociales. De un modo más general, un paradigma es un esquema conceptual que representa los compromisos compartidos de un grupo y que le ofrece al grupo una forma de atender a los fenómenos (Kuhn, 1970b). La noción es suficientemente flexible como para tener mucha aplicabilidad teórica e histórica, pero es demasiado ambigua como para tratar con los problemas filosóficos relativos a la explicación, la justificación y el significado. A pesar de un declarado deseo de evitar la subjetividad total, Kuhn no ha tenido éxito en exponer cómo pueden evaluarse racionalmente los paradigmas o cómo pueden relacionarse a la misma palabra diferentes paradigmas o, aún, qué le representa a un paradigma el ser usado en la resolución de un problema. Masterman (1970) distinguió no menos de veintiún sentidos de "paradigma" en los escritos de Kuhn. No se ha tomado en consideración cómo pueden descubrirse o modificarse los paradigmas. Las ideas de Kuhn sobre la estructura del conocimiento científico son, no obstante, ricas y sugerentes; secciones subsiguientes de este capítulo muestran cómo puede concretarse en términos computacionales.
[37] 3.2.3. La concepción de teoría de conjuntos
Recientemente, ha sido propuesta y desarrollada por diversos autores (Suppes, 1967; Suppe, 1972, 1977; van Fraasen, 1972, 1980; Sneed, 1971; Stegmüller, 1979) una poderosa concepción en (ver) teoría de conjuntos. A diferencia de los testimonios positivista y de paradigmas, esta concepción no ha recibido todavía un análisis crítico sostenido, y no se intentará realizarlo aquí.
En la concepción de teoría de conjuntos, una teoría es una estructura que sirve para seleccionar una clase M de modelos (en el sentido de Tarski; véase el tutorial B) de una clase de modelos posibles Mp . Desde la visión positivista, consideraríamos a M como aquellos elementos de Mp que satisfacen los axiomas de la teoría. Pero, sin tal especificación, generalmente podemos hablar de una teoría como una estructura <K, I> en la que K se dice que es el núcleo de la teoría consistente en el par <M, Mp> tal que M es un subconjunto de Mp, e I es el conjunto de los modelos que son aplicaciones tentativas de la teoría, siendo I un subconjunto de Mp. Una teoría construida con semejante estructura no puede decirse que sea verdadera o falsa, pero puede usarse para formular la afirmación empírica de que los modelos que constituyen las aplicaciones tentativas de la teoría están entre los modelos seleccionados por la teoría: I es un subconjunto de M.
El conjunto M se caracteriza mediante la definición de un predicado P de teoría de conjuntos. Definimos "x es un P" (p.e.: "x es un grupo" o "x es una partícula mecánica clásica") formulando en teoría de conjuntos informal una serie de axiomas que caracterizan aquellos objetos que caen bajo el predicado P. Una afirmación empírica por tanto tiene la forma "a es un P" donde a es una aplicación tentativa.
Esta aproximación a la naturaleza de las teorías parece tener varias ventajas respecto del testimonio positivista. El uso de la teoría de conjuntos informal en vez de la sintaxis formal, facilita la reconstrucción rigurosa de teorías científicas, ya que la caracterización más flexible de un predicado en teoría de conjuntos se ejecuta con mayor facilidad que la axiomatización en la sintaxis formal. Además, el uso de la teoría de conjuntos evita la relatividad lingüística que implica tener una teoría caracterizada en un lenguaje formal específico. (De igual manera, mi enfoque computacional no asigna ninguna significación particular al lenguaje de representación que usa PI para formalizar el conocimiento científico. El rasgo característico del modelo computacional no es un testimonio canónico del conocimiento científico, sino sólo una aproximación a lo que se halla en la cabeza del científico: qué elementos son las estructuras de datos, las cuales pueden implementarse en una cantidad de lenguajes.) Más aún, los trabajos de Sneed y Stegmüller sugieren que los formalismos propios de la teoría de conjuntos pueden manejar la dinámica del desarrollo de las teorías con mayor riqueza que los formalismos sintácticos.
Sin embargo, debemos preguntarnos si las elegantes reconstrucciones formales ofrecidas por el enfoque de la teoría de conjuntos son lo que se espera de un testimonio que dé cuenta de la naturaleza de las teorías científicas. Mi principal objeción se vincula con la adecuación práctica: ¿cuál es la relación entre las estructuras de las teóricas de modelos descriptas arriba y las estructuras cognitivas empleadas por los científicos? [38] El testimonio que se basa en la teoría de conjuntos, al igual que el testimonio positivista, ofrece una descripción muy idealizada de las teorías. Estas idealizaciones pueden ser útiles para tratar problemas filosóficos aislados, pero difícilmente sirvan para caracterizar el uso de las teorías por los científicos. Una teoría tiene que tener alguna relación con el modo en que los científicos realizan la investigación y el testimonio de la teoría de conjuntos es una abstracción muy alejada de las realidades conceptuales. Esto se hace especialmente evidente en las teorías menos matemáticas que los ejemplos de la física tratados por Stegmüller y Sneed, tales como la teoría de la evolución de Darwin. Por supuesto que las teorías matemáticas son muy importantes en la ciencia, en campos tan diferentes como la genética de poblaciones y la microeconomía, al igual que la física. Pero aún en estos campos necesitamos una técnica para representar las conexiones conceptuales que llegan más allá de la formalización de la teoría de conjuntos. La concepción de la teoría de conjuntos es insuficientemente semántica: es necesario caracterizar las conexiones entre los significados en términos más elaborados. E incluso está en peores condiciones que la concepción sintáctica, ya que no llega a sugerir un testimonio de procesos como la resolución de problemas y el descubrimiento porque no dice nada acerca de cómo se transforman las partes de los modelos.
El testimonio de la teoría de conjuntos enfrenta, además de su inadecuación práctica, limitaciones filosóficas. Su abstracción respecto de los elementos pragmáticos del contexto y de la organización epistémica, le crea grandes impedimentos para tratar adecuadamente la explicación y a la inferencia. En particular, el isomorfismo de la teoría de conjuntos no captura de modo adecuado la noción de explicación (ver van Fraasen, 1980).
3.3. Un informe computacional acerca de la naturaleza de las teorías
3.3.1. Reglas y conceptos
El capítulo 2 describía cómo representa PI el conocimiento usando reglas organizadas por conceptos. Ahora quiero mostrar de qué modo pueden contribuir estas estructuras a un testimonio de la naturaleza del conocimiento científico, que sea a la vez razonablemente preciso y suficientemente rico, como para poder dar cuenta de los diversos roles de las teorías científicas.
Centrarse en las reglas sólo, puede sugerir que las teorías en PI no son más que estructuras sintácticas semejantes a los conjuntos de oraciones que, según los positivistas lógicos, constituyen las teorías científicas. Por otra parte, se podría pensar que la resolución de problemas teóricos y la explicación tienen el carácter directamente deductivo subrayado por los positivistas, ya que el desencadenamiento de las reglas es, desde la raíz, una aplicación del modus ponens, una inferencia de si p entonces q y p, hasta q.
Estaríamos tentados a decir que todo lo que se necesita para un enfoque computacional de las teorías es tratarlas como reglas en un sistema deductivo, tal como Prolog o un sistema de producción simple.Tal conclusión, sin embargo, descuidaría las puntualizaciones realizadas en el último capítulo sobre la importancia de los conceptos para agrupar reglas y [39] ayudar a controlar el procesamiento de la información durante la resolución de problemas y el aprendizaje. Los conceptos serían innecesarios si pudiésemos considerar todas las posibles deducciones de todas las reglas existentes, pero ya hemos visto que esto computacionalmente no es factible. La gente parece tener, y los programas parecen necesitar, la capacidad de organizar el conocimiento de tal modo que lo pueda aplicar en las situaciones apropiadas. Los conceptos no sólo organizan reglas que puedan ser aplicadas con eficiencia, sino que, además, organizan el almacenamiento de las soluciones a los problemas, en formas que para la resolución analógica de problemas resultan decisivas.
De igual modo, sería un error argumentar como sigue: "Un programa de computación es, para la computadora en que se ejecuta, una entidad puramente sintáctica, de manera que no hay una diferencia real entre los testimonios computacionales y los testimonios sintácticos de los positivistas lógicos". Aquí hay una confusión de niveles. Desde luego que un programa es una entidad sintáctica, pero el procesamiento puede guiarse mediante estructuras de datos que se comprenden mejor en términos semánticos y pragmáticos. La semántica proviene de las interrelaciones de reglas y conceptos y del mundo (véase capítulo 4 para una discusión sobre el significado); y la pragmática proviene del papel decisivo de los objetivos y el contexto en la determinación del curso del procesamiento.
Permítaseme, para ser más preciso, describir una teoría simple pero importante, la teoría ondulatoria del sonido, cuyo descubrimiento se ha simulado en PI (véase el capítulo 4). Esta teoría retrocede hasta los griegos, originándose probablemente con el estoico Crisipo (ver) (Samburski, 1973), si bien la primera exposición sistemática que he podido encontrar es la del arquitecto romano Vitruvio, alrededor del primer siglo de nuestra era (Vitruvio, 1960). Vitruvio usó la teoría de las ondas para explicar algunas propiedades del sonido que eran muy importantes en la construcción de anfiteatros: el sonido se propaga a partir de su fuente y si encuentra una barrera, puede reflejarse hacia atrás, constituyendo un eco. Estos hechos a explicar están representados en PI mediante reglas simples:
Si x es
sonido, entonces x se propaga.
Si x es
sonido y si a x se lo obstruye, entonces x se refleja.
A primera vista, la teoría ondulatoria del sonido puede parecer meramente otra simple regla, como
Si x es un sonido, entonces x consiste en ondas.
Pero hay dos aspectos claves en los que la teoría ondulatoria del sonido difiere de las reglas simples acerca de la propagación y el reflejo del sonido. Primero, como aclarará la exposición sobre la evaluación de teorías, la base para aceptar la teoría ondulatoria del sonido es diferente de las bases para aceptar las otras reglas, que se derivan de observaciones por generalización. Segundo, parte de la teoría ondulatoria del sonido es un supuesto de la idea nueva de las ondas de sonido, que no son observables, de modo que el concepto de una [40] onda de sonido no podría derivarse de la observación. Lo que constituye la teoría ondulatoria del sonido es pues un complejo de reglas y conceptos.
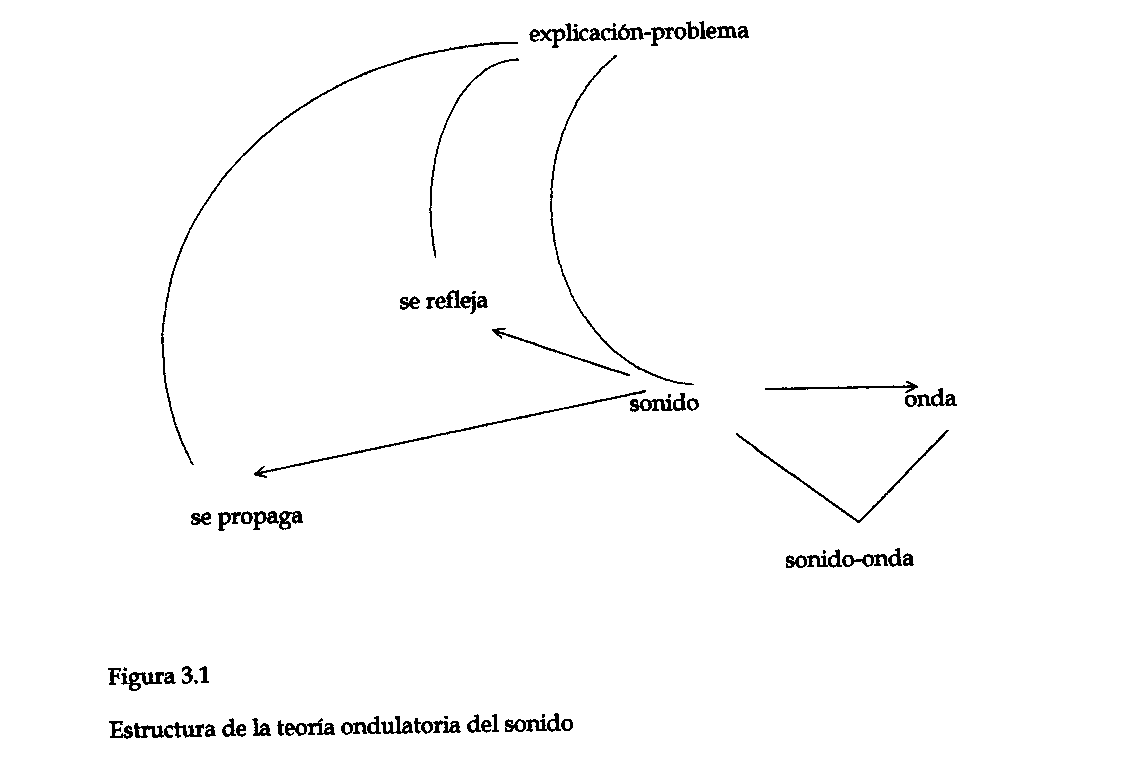
Igualmente importante, la teoría ondulatoria del sonido incluye un registro de sus éxitos anteriores; en este caso, la explicación exitosa acerca de por qué el sonido se propaga y por qué se refleja. Una explicación o la solución de un problema resuelto puede ser complicada, pero seguirle la pista puede ser inmensamente útil en el futuro para resolver problemas semejantes. Una teoría, por tanto, no es una estructura de datos explícita como una regla o concepto, sino un conjunto de estructuras asociadas. Respecto de la teoría ondulatoria del sonido, ésta incluye:
|
Teoría ondulatoria del sonido: |
|
|
Conceptos: |
sonido, onda |
|
Concepto teórico: |
onda-sonora |
|
Reglas: |
Si x es sonido, entonces x
es una onda. |
|
Solución del problema: |
Explicación de por qué se
propaga el sonido. |
La Figura 3.1 describe el complejo de estructuras interrelacionadas que componen la teoría ondulatoria del sonido, una vez que el intento de explicar por qué el sonido se refleja y se propaga llevó a la formación de la nueva regla, según la cual los sonidos son ondas. El nuevo concepto, onda-sonora, formado mediante combinación conceptual (véase sección 4.3), está subordinado a los conceptos de sonido y onda. La nueva solución al problema de explicar por qué el sonido se refleja y se propaga está almacenado, con vínculos con los conceptos de sonido, propagarse y reflejarse.
[41] 3.3.2. La importancia de los esquemas
En el capítulo 2, describí cómo PI forma esquemas de resolución de problemas y cómo ello mejora mucho la realización de la resolución de problemas. Esta ventaja se advierte especialmente en relación con las teorías, que proporcionan de manera invariable esquemas explicativos ricos. Recuérdese que la función principal de una teoría es explicar diferentes leyes, que, a su vez, generalizan numerosas observaciones. Una teoría incluirá, por lo general, un conjunto restringido de principios que se aplican de modo semejante para explicar cada ley y, por extensión, los acontecimientos particulares que caen bajo las leyes.
Kitcher (1981) detalla cómo la explicación teórica consiste en proporcionar unificaciones de fenómenos usando el esquema de la resolución de problemas (ver). Describe cómo Darwin explicó muchos fenómenos diferentes usando patrones semejantes basados en la evolución por selección natural. Darden (1983, p. 156) ha mostrado el poder de un esquema de selección aún más general, aplicable más allá de las selecciones artificial y natural, con los siguientes componentes:
1. Se genera un conjunto de variantes.
2. Se procede a la selección de un subconjunto de variantes.
3. Después de la selección, la combinación de variantes es diferente.
Este es un esquema explicativo poderoso, que ha sido aplicado en muchos dominios, incluyendo el del desarrollo del conocimiento (véase capítulo 6).
De la misma manera Newton explicó muchos fenómenos, usando un esquema que Kitchner (p. 517) describe aproximadamente como:
1. La fuerza sobre a es b.
2. La aceleración de a es g.
3. Fuerza = masa
Citando a Kitchner (1981, p. 517), "Las instrucciones de llenado nos dicen que todas las ocurrencias de ‘a ‘ deben reemplazarse por una expresión que se refiere al cuerpo bajo investigación; las ocurrencias de ‘b ‘ deben reemplazarse por una expresión algebraica que se refiere a una función de las coordenadas de la variable y del tiempo; ‘g ‘ debe reemplazarse por una expresión que proporcione la aceleración del cuerpo como una función de sus coordenadas y de sus derivadas temporales; ‘d ‘ debe reemplazarse por una expresión que se refiera a las coordenadas de las variables del cuerpo, y ‘q ‘ debe reemplazarse por una función temporal explícita." Se puede instanciar Este modelo puede ejemplificarse como para aplicarlo a muchas clases diversas de fenómenos mecánicos. El esquema de Kitcher es más complicado desde el punto de vista matemático, que el que es capaz de manejar PI, pero su función general es la de los esquemas de resolución de problemas, como el esquema de convergencia que PI deriva de sus soluciones a los problemas del rayo y de la fortaleza.
[42]La formación de los esquemas de problemas implica, como hemos visto con el esquema de convergencia, algún tipo de abstracción. Tales abstracciones son importantes en las explicaciones científicas, en las cuales las idealizaciones se usan con frecuencia. Los científicos hablan alegremente de planos inclinados sin fricción, de objetos que caen sin que el aire ofrezca resistencia y de gases ideales. Desde el punto de vista de las teorías científicas como sistemas axiomáticos, puede ser difícil comprender estas expresiones. Pero la idealización cobra sentido cuando se considera a la teoría como parte de un sistema de procesamiento que usa reglas por defecto y esquemas abstractos de resolución de problemas para generar las explicaciones.
La concepción recién explicada también tiene la virtud de ser compatible con los resultados empíricos de Chi, Feltovich y Glaser (1981). Establecen que los expertos difieren significativamente de los novicios en el modo de categorizar problemas físicos y teorizan que las habilidades de los expertos son el resultado de su posesión de esquemas de problemas superiores. Mientras que los novicios tienden a categorizar los problemas por rasgos superficiales, tales como "bloques sobre planos inclinados", los expertos tiende a clasificarlos según los principios físicos principales que gobiernan la solución de cada problema. Durante los experimentos de solución de problemas, los expertos se toman más tiempo que los novicios para clasificar los problemas, pero sus clasificaciones son mucho más efectivas para conducir a soluciones. El conocimiento de la física aquí obviamente va mucho más allá de un conjunto de expresiones abarcadoras de los principios de la física, con los que los novicios también están familiarizados. lo que le falta a los novicios es el conocimiento procesual acerca de cómo y cuando aplicar esos principios, conocimiento que está más apropiadamente codificado en los esquemas de problemas.
3.4. Adecuación práctica del enfoque computacional
En la última sección, se analizaron las teorías como conjuntos de reglas, conceptos y soluciones de problemas. La adecuación práctica de tal enfoque se evidencia por su habilidad para explicar los resultados experimentales de la solución de problemas, superior a la de modelos alternativos. Pero también es interesante ver cómo sirve el modelo para dar cuenta de fenómenos más anecdóticos.
Para comenzar, regresemos a la notoriamente vaga noción de Kuhn acerca de un paradigma. Kuhn (1970b) usó con frecuencia el término "paradigma" para referirse a una teoría o visión del mundo, como el paradigma Newtoniano. Este uso se ha extendido mucho, pero es diferente de la comprensión pre-kuhniana de un paradigma como un modelo general o ejemplo, como puede ser el caso, de la conjugación de un verbo. En el pos-escrito a la segunda edición de La estructura de las revoluciones científicas, Kuhn la menta el uso del término "paradigma" simultáneamente para una general visión científica del mundo y para los ejemplos concretos de soluciones de problemas que, Kuhn argumentaba , eran ampliamente responsables de la construcción de determinada visión del mundo. Él caracteriza este último concepto de paradigma como "el elemento central de lo que ahora considero el más novedoso y menos entendido aspecto" del libro (1970b, p. 187). Propone el término "ejemplar" para las [43] concretas soluciones de problemas que llega a considerar el "más fundamental" sentido de "paradigma" (Kuhn, 1977, p. 298).
Kuhn rechaza la opinión común de que los estudiantes aprenden una ciencia aprendiendo una teoría junto con las reglas para aplicarla a los problemas. Más bien, aprenden una teoría construyendo los problemas, resolviendo los problemas subsiguientes modelándolos sobre ejemplares - de - soluciones previas. Aprender una fórmula teórica, como "F = ma" tiene menos importancia, comparado con aprender las manipulaciones complejas necesarias para resolver diversos problemas acerca de la caída libre, el péndulo y otros. Los estudiantes que afirman que conocen la fórmulas pero que son incapaces de resolver los problemas han perdido el enfoque: conocer la teoría es ser capaz de resolver los problemas. Al esforzarse en trabajar los problemas generales, los estudiantes pueden asimilar lo que Kuhn llama un "modo de trabajar evaluador - del - tiempo y autorizador - del - grupo" (Kuhn, 1970b, p. 189).
Un modelo computacional como PI puede captar tanto los aspectos ejemplares como de la visión del mundo de la práctica científica. El mecanismo de PI par resolver y almacenar problemas posibilita justamente la clase de solución analógica de problemas a las que Kuhn apunta. Los ejemplares son soluciones exitosas de problemas que se almacenan con conceptos de importancia. Si se han usado frecuentemente tales ejemplares, pueden abstraerse y almacenarse con esquemas de problemas como la abstracción a partir de los problemas del rayo y la fortaleza descriptos en la sección 2.3.2. Una red conceptual completamente abierta, con muchas soluciones de problemas almacenadas, constituiría un paradigma en el sentido más amplio de Kuhn, proporcionando una especie de visión del mundo, un modo sistemático de aproximarse a los problemas del mundo. La existencia de tal red no necesita permanecer como una vaga hipótesis, ya que puede ser simulada en modelos computacionales con un suficientemente rico conjunto de estructuras de datos, que incluyen conceptos y soluciones de problemas. Por ello resulta posible dirigir tales propuestas filosóficas con mayor precisión que la alegada inconmensurabilidad de las teorías rivales (capítulo 5) y el conservadurismo metodológico de los proponentes de una teoría (capítulo 8).
Esto completa mi argumento respecto de la adecuación práctica del enfoque computacional a las teorías científicas, ya que el informe acerca del descubrimiento científico en el capítulo 4 también es relevante. La adecuación histórica se discute en los capítulos 4, 5, 6 y 8. El intento de mostrar que un enfoque computacional de las teorías es más adecuado filosóficamente que las alternativas comienza ahora con una discusión de la explicación científica.
3.5. Explicación
La explicación científica de un fenómenos observado es una de las actividades científicas más importantes. Gran parte del trabajo actual en filosofía de la ciencia se refiere a proporcionar condiciones necesarias y suficientes para una explicación científica. El foco principal de esta discusión ha sido el poderoso modelo deductivo - nomológico de explicación de Hempel (1965), descrito en el [44] tutorial A. Yo no intentaré resumir aquí todas las críticas a este modelo, pero en vez de ello desarrollaré un concepto alternativo de explicación acorde con el enfoque computacional de las teorías antes esbozado. Ya que la mayoría de los conceptos en lenguaje natural no son susceptibles de definirse según condiciones necesarias y suficientes, sería un desatino intentar proporcionar tales condiciones para la explicación. En realidad, el enfoque de la formación de conceptos asociado con los enfoques procesuales que he desarrollado sugieren que el análisis conceptual debe servir para caracterizar lo que se conoce habitualmente, más que universalmente, acerca de una noción.
El término "explicación" es muy ambiguo. Hempel y otros lo usan para referirse a una estructura sintáctica consistente en oraciones deductivamente relacionadas que incluyen el explanans y el explanandum. En el discurso informal, con frecuencia se entiende por "explicación" una teoría que forma parte de una explicación en sentido hempeliano: la teoría newtoniana es una explicación de las mareas. Yo quiero explorar un tercer sentido del término, en el cual la explicación no es una estructura explicativa, ni algo que explica, sino un proceso que proporciona comprensión. La explicación es algo que la gente hace, no una eterna propiedad de conjuntos de oraciones. (Nota: este sentido de "explicación" debe distinguirse de un sentido que se ha hecho común en IA relativo al "aprendizaje basado en la explicación", según el cual un explicación es una descripción de cómo un programa alcanza determinado resultado.)
3.5.1. Comprensión
Explicación es un proceso para proporcionar o alcanzar comprensión, pero ¿qué es comprensión? En general, comprender un fenómeno es encuadrarlo en un modelo o contexto previamente organizado. Pero esta caracterización no es informativa, sin especificar la naturaleza de los modelos y contextos. Gran parte de la plausibilidad del modelo deductivo - nomológico de Hempel proviene del modo preciso en que un sistema lógico, en el cual una teoría es un conjunto de oraciones y la explicación es una deducción a partir de esos axiomas, proporciona un contexto estructurado y bien comprendido. Veremos cómo un enfoque computacional puede proporcionar las mejores formas de estructura y contexto.
Desde un punto de vista computacional, comprender un acontecimiento es recuperar de la memoria una estructura de conocimiento que se materializa en el acontecimiento (cf. Schank y Abelson, 1977). Para entender una frase como "John empujó su carrito hacia el cajero y sacó el jabón", un individuo debe activar una estructura (marco, libreto, esquema) que describa el comportamiento habitual en un supermercado. Las pistas en el marco SUPERMERCADO se corresponden con la información proporcionada en la frase y la información adicional contenida en el marco puede usarse para responder preguntas acerca del comportamiento de John descrito en la frase. Un programa adecuado podría responder a "¿Por qué John sacó el jabón de su carrito?"aplicando el conocimiento incorporado en el marco citado, acerca de que en un supermercado uno habitualmente [45] lleva su carrito a una caja, pone los ítems del carro sobre el mostrador y paga por los ítems. Derivar una respuesta para la pregunta es relativamente fácil computacionalmente, una vez que se ha encontrado el marco apropiado. El paso clave para alcanzar la comprensión es el procesual de recuperar un marco que se corresponda con los aspectos centrales del acontecimiento a explicar. Aquí, la explicación no consiste en referirse a leyes implicadas o generalizaciones estadísticas inespecíficas, sino en la aplicación de una estructura que describe sucesos habituales. Comprender se logra fundamentalmente mediante un proceso de ubicación y correspondencia, más que de deducción.
Esta consideración se ajustará mejor si se han compilado previamente los marcos relativos a todos lo acontecimientos que habrán de explicarse. Pero no puede dar cuenta de nuestra habilidad para proporcionar explicaciones acerca de un único o inhabitual suceso. Supóngase que se quiere explicar por qué John se sacó toda su ropa en el supermercado. El marco supermercado y el marco de desvestirse no serán de mucha ayuda. Apuntando a una flexibilidad incrementada, Schank (1982) propone que el conocimiento debe organizarse en estructuras menores a las que llama "paquetes de organización de memoria". PI gana en flexibilidad asociando a los conceptos diversas reglas, que pueden, una vez activadas, trabajar independientemente para generar una explicación. Así las explicaciones de PI implican tanto la correspondencia con una situación, en cuanto los conceptos relevantes se han activado, como la deducción, en cuanto se han disparado las reglas. Este proceso puede describirse como la aplicación de un "modelo mental" construido para una situación (Holland et al., capítulo 2).
3.5.2. Explicación y solución de problemas
En PI, la explicación es una clase de solución de problemas y la descripción de cómo trabaja el programa ayudará a mostrar las relaciones entre esas dos importantes actividades científicas. Un problema se especifica proporcionando sus condiciones iniciales y los objetivos que deben alcanzarse. Una solución de problema es un conjunto de pasos, simulados o efectivamente realizados, que conducen desde las condiciones iniciales al objetivo. En PI, la clase más simple de un problema de explicación es aquel en el que los objetivos no son estados que deben alcanzarse, sino estados que se sabe que son ciertos. Sin embargo, el proceso de descarga de las reglas para generar los objetivos es el mismo, con una importante diferencia: mientras en la solución de problemas PI proyecta acciones, en la explicación PI forma hipótesis que pueden conducir a una explicación. Para ser concretos, imagínese que su problema consiste en ayudar a su jefe de departamento a calcular como llegar a Chicago. Usted puede proyectar diversas acciones que lo o la llevarán desde su departamento a Chicago. Estructuralmente, tenemos:
|
PROBLEMA: |
|
|
ORIGEN: |
N es el jefe del Departamento de Taxidermia |
|
OBJETIVO: |
N está en Chicago |
En un problema más realista, el conjunto de condiciones iniciales sería significativamente [46]mayor y los objetivos incluirían restricciones adicionales acerca de lo que constituiría una solución del problema.
La explicación análoga tendría una estructura semejante, con un "explanandum" (lo que hay que explicar) en el lugar del objetivo:
|
PROBLEMA - DE - EXPLICACIÓN |
|
|
ORIGEN: |
N es el jefe del Departamento de Taxidermia |
|
EXPLANANDUM |
N está en Chicago |
Aquí, usted trataría de usar lo que sabe acerca de N, acerca de su Departamento y acerca de Chicago para generar una respuesta acerca de por qué N está en Chicago.El mismo mecanismo general de activación de expansión y descargue de reglas que habilitan a PI a calcular cómo llevar a N a Chicago también generarán una explicación acerca de por qué N está allí, excepto que, en vez de producir las acciones proyectadas, el programa genera las hipótesis posibles (tales como que N está en una conferencia) que puedan proporcionar una explicación. Más desarrollo acerca de cómo PI genera hipótesis está en el capítulo 4.
La semejanza estructural entre la explicación y la solución de problemas resulta clara a nivel de la explicación de hechos particulares, tales como la ubicación de N. Pero la explicación científica concierne no sólo a hechos particulares, sino también a leyes generales. La clase de explicación y solución de problemas expuesto hasta aquí es una parte significativa de la práctica científica cotidiana, pero desde un punto de vista global y epistémico, otro nivel de la explicación es más importante. Se trata de la explicación de modelos generales de acontecimientos, más que la ocurrencia de acontecimientos particulares. Tal explicación ha sido entendida habitualmente con la deducción de generalizaciones empíricas a partir de teorías axiomatizadas. Las leyes de Kepler acerca del movimiento de los planetas se dijo que pueden derivarse de la mecánica newtoniana; la refracción óptica puede explicarse derivando la ley de Snell ya bien de las teorías de ondas o de la de partículas, etc. Volvamos a un ejemplo que es suficientemente simple como para que PI lo considere. La teoría ondulatoria del sonido tiene que explicar la ley general de que el sonido se propaga, cuya más simple expresión es una regla con la condición (sonido (x) verdad) y la acción (se propaga (x) verdad). Explicar esta regla es simple. PI crea un problema usando un objeto arbitrario x:
|
PROBLEMA - DE - EXPLICACIÓN: |
|
|
ORIGEN: |
x es un sonido |
|
EXPLANANDUM: |
x se propaga |
Por tanto, incluso la explicación de acontecimientos puede comprenderse en PI mediante los diversos mecanismos de solución de problemas (ver sección 2.3.2. y el apénide 2 para detalles). Es fácil con el marco computacional bloquear las [47]explicaciones triviales, tales como que x se propaga justamente porque es sonido, o que se propaga porque se propaga.
Pero hay más acerca de la explicación de lo que hasta aquí sugeriría la exposición sobre la solución de problemas. Adaptando un ejemplo de Bromberger (1966), podríamo asignar a un estudiante el problema de calcular la altura de un mástil, dada la longitud de su sombra, fórmulas trigonométricas y la ley de la propagación rectilínea de la luz. El cálculo del estudiante de que le mástil tenía n pies de alto resolvería el problema, pero no explicaría por qué el mástil tiene n pies de alto. El cálculo no nos proporciona la comprensión de por qué el mástil tiene la altura que tiene.
Tal comprensión requiere más rasgos contextuales y es fácil ver cómo el sistema PI puede proporcionarlos. Tenemos mucha información de base acerca de los mástiles, en especial acerca de las causas de su construcción. Presumiblemente, el concepto de mástil contendrá una regla acerca de que los mástiles son objetos manufaturados. Al activar el concepto de los objetos manufacturados, se dispondría de la regla acerca de los diseñadores y fábricas que producen tales objetos. Así los procesos subordinados de PI nos conducirían a buscar los diseñadores y fábricas que produjeron el mástil e incluso más allá hacia una explicación de por qué los diseñadores lo planearon tal como lo hicieron. Las reglas de la trigonometría y del comportamiento de la luz, normalmente, no se activarían en absoluto. Establecer el problema con él como parte de las condiciones iniciales es un mal chiste.
Aunque no es probable que produjera tal derivación, PI habitualmente no tiene los recursos para rechazar una derivación acerca de la altura del mástil usando su sombra como una no-explicación. Su instrumental de solución de problemas, si éste fuera el conocimiento relevante y si no se encontrara la explicación apropiada basada en el diseño humano, llegaría y aceptaría la información de la sombra. El problema es que habitualmente, PI carece de suficiente comprensión de la causalidad. Como plantea Brody (1972)
es plausible suponer que lo que diferencia las explicaciones reales del ejemplo del mástil y de otros contraejemplos respecto del modelo nomológico-deductivo es la referencia a un rasgo causal o esencial. De modo semejante, Hausman (1982) ha planteado que las asimetrías causales son la clave para ver por qué la altura del mástil no puede explicarse usando la longitud de la sombra: nuestro conocimiento básico nos dice que la altura de los mástiles determina el largo de las sobras, no a la inversa. PI necesita poder adquirir una clase de conocimiento que habitualmente le falta, implicando conocimiento de alto nivel acerca de qué clases de cosas causan qué. La adquisición de tales "esquemas causales" requerirá una habilidad para distinguir entre las generalizaciones accidentales basadas en mera coocurrencia de cosas y las conexiones causales genuinas. Tal comportamiento requerirá una comprensión mucho más profunda de la causalidad de la quie PI o cualquier otro programa de IA tiene, tomando en cuenta factores tales como la prioridad temporal y modelos de interconectividad entre clases de acontedimientos (Hausman, [48] 1984) La ventaja de un enfoque computacional frente a otro mucho más austero sintácticamente es que sería posible enriquecer a PI para que pueda adquirir y usar tal conocimiento.Los críticos han utilizadfo el ejemplo del mástil para argumentar que el modelo nomológico-deductivo de explicación es demasiado blando, pero también han acusado al modelo de ser demasiado estricto es su constante requerimiento de leyes. PI puede aprender clases mucho más blandas de explicaciones, ya que las reglas que usa en sus explicaciones no necesitan ser lleyes generales: sólo necesitan expectativas normales acerca de lo que ocurrirá.
Obviamente, el informe esbozado hasta aquí, todavía no proporciona las condiciones suficientes para una buena explicación científica. La toelogía, la astrología y cualquier otra cosa puede decirse que proporcionan explicaciones en el sentido débil de utilizar reglas y conceptos para generar conclusiones. La gente tiene sistemas conceptuales para toda clase de mitologías e ideologías y nosotros quisiéramos diferenciar las explicaciones que ellos proporcionan de las explicaciones correctamente valoradas en la cienca. Sin embargo, esta tarea concierne a temas epistemológicos que van más allá del tema de la estructura de las teorías y las explicaciones. No creo que podamos diferenciar en general acerca de los fundamentos estructurales entre los sistemas y explicaciones de la ciencia y los de las pseudociencias y no-ciencias. Como veremos en el capítulo 9, la demarcación es un tema complicado del contexto histórico de una disciplina, incluyendo la presen cia de teorías competitivas y la información temporal de la disciplina. La teología y la astrología se diferencian de los sistemas científicos en cuanto a la validación, no por la estructura. Un completo informe de la explicación incliría una descripción de las condiciones epistémicas que un sistema de conceptos y reglas tiene que encontrar antes de que lo honremos como plenamente explicativo. Candidatos a tales condiciones incluyen la verdad, la confirmación y ser la mejor teoría disponible. El Capítulo 5 muestra cómo estas condiciones puede aplicarse a sistemas tales como PI. En este parágrafo, he estado usando el sentido honorífico de "explicación" en el que decimos que sólo explica una buena (verdadera, aceptable, confirmada) teoría. La exposición previa intentó captar el sentido más general de "explicación", en el que podemos decir que explica una teoría falsa.
He entrado en cierto dcetalle acerca de la explicación para mostrar cómo un informe computacional puede contribuir a la comprensiòn filosófica. El intento de demostrar la superioridad filosófica de un informe computacional acerca de las teorías continúa en los siguientes capítulos que consideran los procesos por los que las teorías se descubren y justifican.
3.6. Resumen
Una teoría científica puede construirse como un sistema computacional de conceptos, reglas y soluciones de problemas. Este constructo tiene varias ventajas sobre los [49] enfoques habituales de las teorías como sistemas de axiomas o estructuras de conjuntos teóricos. En particular, podemos describir como un sistema computacional dirige la práctica cotidiana de los científicos en la solución de problemas, usando esquemas adquiridos de anteriores soluciones de problemas. En estos términos, pueden entenderse las complejas funciones de los paradigmas de Kuhn. A un nivel más filosófico, también podemos proporcionar un encuadre cognitivo de la explicación teórica en cuanto resolución de problemas utilizando esquemas explicativos.
[51] Capítulo 4
Descubrimiento y emergencia del significado
4.1. Introducción
[A partir de aquí, la traducción sintetiza, provisionalmente (27-01-03), el texto, seleccionando lo esencial para conservar el desarrollo del pensamiento de Thagard]
Las teorías difieren de las generalizaciones empíricas en que sirven para explicar tales generalizaciones y lo hacen postulando entidades inobservables. Se enfrentan dos graves problemas: ¿cómo pueden descubrirse las teorías? y ¿cómo pueden ser significativos los conceptos que emplean?
Recientemente ha habido mucha discusión acerca de si existiría una "lógica del descubrimiento". Reichenbach (1938) propuso una distinción terminante entre contexto de descubrimiento y contexto de justificación. La relación entre justificación y descubrimiento ha permanecido oscura.
Una descripción de la simulación en PI. tanto del descubrimiento como de la justificación de las teorías, mostrará como se mezclan descubrimiento y justificación, con lo que se rechaza la distinción de Reichenbach entre lógica de la justificación y la psicología del descubrimiento. No se requiere una terminante distinción entre lógica y psicología. El vínculo entre descubrimiento y justificación de las teorías se establece a través de una forma de razonamiento que Peirce llamó "abducción". Abducción es la inferencia de una hipótesis que proporciona una explicación posible de algún [52] fenómeno problemático. Veremos cómo la abducción puede ser tanto un componente en el descubrimiento de las hipótesis como un ingrediente clave en su justificación.
4.2 Abducción
La abducción es un fenómeno invasivo en la ciencia y en la vida cotidiana.
[53] Cómo planteó Peirce y psicólogos tales como Gregory (1970) y Rock (1983) confirmaron, la abducción juega un papel incluso en fenómenos visuales relativamente simples. Muchos estímulos visuales están empobrecidos o son ambiguos, por lo que la gente se acostumbró a imponerles un orden.
4.2.1 ¿Descubrimiento o justificación?
Si la abducción es un mecanismo para el
descubrimiento o para la justificación ha estado controvertido y el propio
Peirce cambió su pensamiento al respecto. Los editores de la obra de Peirce
enturbiaron la transición de su pensamiento, al incluir la exposición de la
hipótesis bajo el título de la abducción, oscureciendo su cambio desde la
creencia de que la inferencia de una hipótesis explicativa pudiera ser una
clase de justificación, hasta la visión más amplia de que sólo es una forma
de descubrimiento.
Una de las razones principales del cambio en Peirce fue el observar la clara debilidad del método de la hipótesis. Decidió que lo que él llamó inducción, en el que se formulan y se prueban las predicciones, era la única fuente de la justificación.
El programa PI proporcionó un medio para investigar con cierto detalle el proceso de interacción entre el descubrimiento y la justificación de las hipótesis. "Abducción" ha llegado a ser un término de creciente popularidad en inteligencia artificial, pero su significado se amplió más allá de la pretendido por Peirce, hasta abarcar varias clases de evaluación de hipótesis tanto como de formación de hipótesis. PI también es capaz de evaluar hipótesis (capítulo 5), pero aquí nos concentraremos en [54] los mecanismos para la generación de hipótesis. Cuatro clases de abducción se han desarrollado en PI: simple, existencial, formadora de reglas y analógica. La abducción simple genera hipótesis acerca de objetos individuales. La abducción existencial postula la existencia de objetos previamente desconocidos. La abducción formadora de reglas produce reglas que explican otras reglas y, por tanto, es importante para la generación de teorías que explican leyes. Finalmente, la abducción analógica utiliza casos previos de formación de hipótesis para generar hipótesis semejantes a las existentes.
4.2.2 La abducción simple en PI
Los capítulos previos describieron cómo PI
resuelve los problemas mediante un proceso de disparar una regla y ampliar la
activación de conceptos. Durante la solución de problemas aparecen varias
clases de inducción. Básicamente, PI no trabaja todas las inducciones que
puede. Como argumentan Holland et al. (1986, capítulo 1) cualquier sistema
realista de aprendizaje debe ser muy pragmático, limitando sus
inferencias a aquellas que tiene una buena oportunidad de ser útiles para el
sistema. En realidad, los sistemas también deben ser pragmáticos acerca de las
deducciones que formulan, ya que es crucial evitar la explosión combinatoria
que la deducción desenfrenada produciría. PI limita la deducción tomando
sólo en cuenta las reglas y contiendas que surgen de sus conceptos activos. De
modo semejante, limita la inducción focalizando sólo el conjunto de reglas,
mensajes y conceptos efectivamente activados.
Recuérdese que algunos problemas son problemas de explicación: su objetivo consiste en encontrar una explicación a un conjunto de mensajes. La abducción es apropiada cuando el sistema tiene que explicar algún mensaje y existe una regla habitualmente activa que lo explicaría si se formulara un supuesto adicional.
[55] (... Obviamente, la hipótesis de que Michael es un músico de rock no estaba previamente formada, pero llega a estarlo sólo como el resultado de la abducción.) De modo más general, el modelo de inferencia es:
G (a) debe explicarse; o sea, por qué a
es G
Si F (x) entonces G (x); o sea, todas las F son G
__________________________________________
Por tanto, hipotéticamente, F (a); o sea, a es F
[56] La abducción simple en PI incluye casos más complejos que los descritos, ya que PI puede tratar con relaciones de n-lugares, como "ama", y formará hipótesis a partir de cualquier cantidad de condiciones. Si la regla tiene la forma
Si A & B & C & D entonces E
en donde E corresponde a un hecho que debe explicarse, entonces todos los A, B, C y D pueden hipotetizarse.
Los dos elementos cruciales en la formación de una hipótesis son la forma abstracta de la inferencia abductiva y el papel de la activación extendida para hacer disponible la regla relevante. Puede imaginarse la abducción como una especie de inferencia lógica, pero la activación extendida tiene un aroma de mayor pureza psicológica.
4.2.3 La abducción existencial
Una clase importante de inferencias supone que se postule la
existencia de algo no observado previamente. Por ejemplo, la investigación de
Pasteur acerca del contagio de las enfermedades le condujo a postular la
existencia de agentes infecciosos no detectados, y después identificados como
virus.
[57] En PI, la abducción existencial opera de modo semejante a la abducción simple, utilizando una búsqueda entre las reglas activas para explicaciones posibles de explananda dadas.
En general, la abducción existencial se realiza cuando las condiciones de las reglas incluyen predicados relacionales que tienen argumentos, algunos de los cuales no están limitados a usar la información [preexistente] en el explanandum.
(El ejemplo del razonamiento acerca del flogisto para explicar la combustión)
[58] Hay que explicar por qué x pierde peso
(cuando se lo quema)
Si x contiene una sustancia y que se expele, entonces x pierde peso
____________________________________________________________________
Por tanto, existe una sustancia y contenida en x que fue expelida de él
Posteriormente, experimentos más cuidadosos, utilizando recipientes sellados, determinaron que en realidad los objetos ganaban peso durante la combustión, explicación que sugiere la abducción existencial de que existe cierta sustancia (oxígeno) que se combina con los objetos durante la combustión.
4.2.4 La abducción formadora de reglas
¿Cómo haríamos para obtener la abducción
de teorías, que son ellas mismas reglas? Describiré dos modos de utilizar la
abducción para obtener reglas. El primero es problemático y no parece jugar
ningún papel en la formación de las teorías. En él, se postula la regla de
que todo A es B para explicar por qué un A particular es B. El segundo es una
combinación de la abducción y la generalización.
Esta es la clase insatisfactoria. La forma de la inferencia sería:
Michael se viste de modo desaforado
Michael es un músico de rock
__________________________________
Todos los músicos de rock se visten desaforadamente
[59] La inferencia suena razonable en este caso particular, pero añadir estas formas de inferencia en PI producía demasiadas hipótesis débiles. El problema surge en simulaciones mayores en las que se deberán generar muchas reglas, produciendo abundantes conjuntos. Para suprimir la superabundancia de hipótesis es necesario hacer lo que hace PI respecto de la generalización: considerar contraejemplos, cantidad de instancias y variabilidad. Pero entonces la abducción de reglas a partir de hechos es redundante, ya que la regla que forma puede alcanzarse más adecuadamente por generalización, para lo cual la explicación es irrelevante. Por tanto, el mecanismo general de la abducción de reglas a partir de mensajes ha sido eliminado de PI, sin pérdida aparente, ya que las reglas acerca de observables pueden formase por generalización.
Sin embargo, la abducción a partir de mensajes todavía puede tener un papel importante en la producción de nuevas reglas. La abducción de reglas trabaja así: si PI construye la abducción de que la F que es x es también H, porque esto explicaría por qué es G, puede por tanto generalizarse que todo F es H. Esto es mucho más restrictivo que la abducción general de reglas que rechacé antes, ya que sólo se aplica cuando ha existido la explicación de un mensaje por otro que contiene una variable universal que representa una instancia arbitraria.
[60] 4.2.5 La abducción analógica
Las variedades de la abducción analógica son
claramente importante en la ciencia. Hanson (1961) describió cómo los
científicos con frecuencia buscan hipótesis particulares, sabiendo que existen
ciertas clases de hipótesis que tienen la posibilidad de ser útiles ya que han
dado resultados en casos semejantes. Cuando una teoría se ha autoconfirmado,
los científicos con frecuencia quieren utilizar clases semejantes de
explicaciones. Por ejemplo, el gran éxito de la mecánica de Newton hizo que la
mayoría de los científicos de los siglos dieciocho y diecinueve se esforzaran
por dar explicaciones mecánicas de los fenómenos.
[61] De modo semejante (a cómo se resolvían los problemas analógicos) las soluciones a problemas pasados pueden sugerir complejos de hipótesis que proporcionarán una explicación en un nuevo caso.
[62] Mientras, en la forma común de la solución analógica de problemas, la analogía se utiliza para construir nuevos sub-objetivos para el problema actual basándose en lo que funcionó en el pasado, la analogía en los problemas de explicación se usa para construir nuevas hipótesis basadas en hipótesis que funcionaron en problemas semejantes. En ambos casos, análogos potencialmente útiles se encontraron mediante la activación extendida y proyectándolos juntos por los rastros de activación entre conceptos análogos.
Por tanto la abducción analógica puede ser importante para la generación de hipótesis que implican más saltos substanciales que la abducción simple, existencial o formadora de reglas.
[63] Vuelvo ahora a la pregunta acerca de si los modelos tales como PI y otros constituirán una "lógica" del descubrimiento.
4.2.6 ¿Lógica del descubrimiento?
Hanson (1958) afirmó que la abducción
constituía una lógica del descubrimiento, pero más tarde se retracto en favor
de una clase de razonamiento que sugería sólo clases de hipótesis
(1961). Salmon (1966sugiere esta distinción triádica, en vez de la dual de
Reichenbach:
1. pensamiento inicial de una hipótesis,
2. establecer que una hipótesis sea plausible,
3. establecer que una hipótesis sea aceptable.
Esta distinción es seriamente deficiente, ya que cada etapa se empaña en la siguiente.
[64] La crítica a la idea de una lógica del descubrimiento sostiene que no puede existir un método mecánico para generar descubrimientos exitosos. Lo que puede decirse es que probablemente no existe en realidad ningún método mecánico práctico para determinar cuándo las proposiciones son tautologías.
Tenemos que estar de acuerdo con las críticas a la idea de una lógica del descubrimiento, en cuanto no existe algoritmo para hacer descubrimiento que garanticen soluciones a los problemas de explicación. Pero puede mantener, sin embargo, que el proceso de descubrimiento es algorítmico, empleando varios algoritmos, como los aplicados por PI, los cuales alientan pero no garantizan la generación de soluciones.
Veremos cómo la abducción repetida de una hipótesis que explica un conjunto de hechos puede contribuir a su justificación.
[65] 4.3 La formación de conceptos teóricos
Peirce pensó que la abducción era una fuente de nuevas ideas, pero esto sólo es verdad respecto de las ideas en el sentido débil de hipótesis, no en el sentido de conceptos.
El problema de cómo pueden surgir nuevos conceptos es especialmente grande respecto de los conceptos teóricos tales como onda de sonido o electrón. El mayor trabajo en el aprendizaje por máquinas está relacionado con cómo los conceptos pueden formarse a partir de descripciones y observaciones. Pero, ¿de dónde provienen los conceptos que pretenden referirse a entidades inobservables? Los filósofos positivistas han querido negar que términos tales como "electrón" puedan ser significativos salvo que sean definidos de algún modo mediante observaciones; vestigios de esto se encuentran todavía en el dicho de muchos psicólogos acerca de la necesidad de "operacionalizar" las ideas. De un modo semejante, los filósofos antirealistas niegan que "electrón" intente referirse a algo, sino que sólo es un instrumento útil para hacer predicciones. Aquí sólo quiero considerar cómo un sistema computacional puede construir conceptos teóricos.
PI tiene un tosco mecanismo para la formación ascendente (botton-up) de conceptos. Para producir un nuevo concepto teórico, sin embargo, se deben combinar conceptos existentes de modo que produzcan conceptos cuyas instancias no son directamente observables. Una noción estricta de conceptos, definidos en función de condiciones observacionales necesarias y suficientes, no permitiría suficiente flexibilidad para hacerlo. Ya que si hay condiciones estrictas de observación para la aplicación de los conceptos A y B, también deberán existir condiciones observacionales de un concepto A-B combinado, que por tanto no es un concepto teórico.
El mecanismo de combinación conceptual de PI es mucho más flexible. La combinación conceptual se activa en las mismas ocasiones que la generalización, cuando dos conceptos activos tiene instancias en común. La mayoría de las combinaciones conceptuales, sin embargo, no son problemáticas ni interesantes. PI sólo forma un nuevo concepto permanente por combinación, [66] cuando los conceptos originales producen expectativas diferentes, en cuanto determinadas por las reglas que se le adjuntan.
Cuando se informa acerca de dos conceptos con instancias comunes y expectativas conflictivas, PI produce en nuevo concepto combinado con reglas que reconcilian el conflicto en la dirección de uno de los conceptos donantes.
[67] Así, un concepto teórico puede surgir juntando combinaciones de conceptos no teóricos.
En virtud de la combinación conceptual y los mecanismos abductivos antes descriptos, PI es capaz de simular la adquisición de una teoría simple cualitativa.
[68] 4.4 La emergencia del significado
¿Cómo llega a ser significativas palabras, ideas, oraciones y otras representaciones? En filosofía de la ciencia, la pregunta central acerca del significado se ha referido a los términos teóricos: ¿cómo pueden tener significado términos como "electrón" que han sido removidos a tanta distancia de la experiencia?
Desde Hume a Carnap, los filósofos positivistas mostraron al significado como emergiendo de la experiencia.
La IA proporciona un conjunto mucho más rico de técnicas para investigar el desarrollo del conocimiento del que disponían los positivistas. Yo propondré que el significado de un símbolo pueda comprenderse a partir de mecanismos computacionales que conducen su construcción y guían su uso.
[69] Aquí está cómo el significado emergería en PI si estuviera equipado con determinada interfaz robótica para detectar rasgos simples en el mundo. La coocurrencia de rasgos activaría la generalización, formando reglas acerca de cómo aquellos rasgos se relacionan uno con otro. La detección de contraejemplos par reglas existentes, conduce a la formación de reglas más complejas por especialización. Simultáneamente, la activación de reglas con el mismo complejo de rasgos en sus condiciones conduce a la formación de nuevos conceptos más elaborados que los detectores de rasgos innatos representados por una clase de formación ascendente (botton-up) de conceptos. El simple mecanismo ahora usado por PI para este propósito sirve para reglas actualmente activas con las mismas condiciones y acciones diferentes; tales pares de reglas indican que algunos conjuntos de propiedades tienen valores generales predictivos.
Conceptos mucho más lejanamente removidos de los detectores innatos pueden formarse por combinación de viejos conceptos. Cuando se forman nuevos conceptos, se hacen posibles nuevas generalizaciones y abducciones empleando esos conceptos. los resultados son conceptos y reglas que no se relacionan con el mundo de ningún modo directo, pero heredan el significado a través del proceso histórico de inducción de nuevas estructuras.
[70] En PI, el significado de un término reside en su papel funcional, el cual está determinado por las reglas y conceptos con los que aparece el término. El significado no está fijado por definición, ya que raramente hay alguna. Más bien, el papel de un concepto depende de las reglas que se han formulado utilizándolo y con qué otros conceptos está relacionado mediante reglas y relaciones de subordinación/superordinación.
En PI, el papel computacional de un concepto, como jirafa, está especificado mediante los procesos que operan con él, lo que habitualmente incluye:
1. activación extendida a conceptos
subordinados y superordinados,
2. mensajes y reglas activados que conducen a la activación de reglas y, por su
intermedio, a la activación de conceptos adicionales,
3. activación de soluciones a problemas pasados análogos al actual,
4. activación de inferencias inductivas que pueden conducir a nuevos conceptos,
reglas o mensajes.
Por tanto, el concepto está inmediatamente listo para funcionar en las inferencias del sistema, tanto en la solución de problemas como en la activación de nuevas inducciones.
La adquisición de un concepto en ciencia o en la vida cotidiana requiere conectarlo de diversos modos inductivos, jerárquicos, no-definicionales, con otros conceptos. Así es como emerge el significado.
[71] 4.5 Lo innato
Para concluir mi discusión sobre el descubrimiento, quiero considerar el papel que lo innato puede tener en la abducción y la formación de conceptos. La aprobación de Chomsky (1972) respecto de las ideas de Peirce acerca de la abducción deriva en parte de algunos enfoques semejantes que tienen acerca de lo innato. Chomsky plantea que nuestras abducciones relativas a las reglas de la gramática están fuertemente guiadas por el conocimiento innato relativo a los universales del lenguaje. De forma más general, Peirce sostiene que la abducción respecto de las hipótesis científicas sería imposible si la naturaleza no nos hubiera dotado con alguna facultad especial para hacer buenos conjeturas. Indudablemente, cada individuo comienza con al menos algún concepto innato producido por la evolución, por ejemplo, acerca de las relaciones espaciales. Quizá también existan reglas gramaticales innatas. La dimensión de este repertorio innato es una cuestión empírica.
Pero también puede ser que el equipamiento innato que tenemos para solucionar los problemas cotidianos y para la formación de hipótesis sea todo lo que también necesitamos para el lenguaje y la ciencia. Quizá sea suficiente con algo semejante a los mecanismos de PI para dirigir la expansión de la activación y la activación de las inducciones para encuadrar el aprendizaje. Que existan preferencias por ciertas clases de hipótesis basadas en el conocimiento innato tiene cierta plausibilidad respecto de cosas básicas como moverse alrededor en nuestro entorno e incluso quizá respecto del lenguaje. Pero no resulta en absoluto claro que tengamos alguna facultad especial para conjeturar correctamente cuando se aplica, por ejemplo, a la física teórica. En ciencia, nos hemos esforzado alejándonos suficientemente de las categorías con las que la evolución nos proveyó, de modo que la abducción y nuestro conocimiento acumulado es todo lo que tenemos para trabajar. Afortunadamente, restringir la abducción a la solución de problemas puede tener suficiente fuerza sin acudir a preferencias innatas por determinadas clases de hipótesis. Peirce mostró la necesidad de restricciones respecto de la formación de hipótesis, pero el mecanismo computacional de activar la abducción mediante el estado habitual de activación durante la solución de problemas puede ser todo lo que resulte necesario. Por cierto que una parte importante del desarrollo del conocimiento teórico en la ciencia puede consistir en trascender las inadecuadas categorías perceptuales de espacio y tiempo, en favor de otras más potentes, no-intuitivas y no euclidianas. En la física subatómica corriente, varios teóricos están investigando las propiedades del espacio con diez o más dimensiones y resulta difícil ver cómo sus especulaciones puedes estar controladas por preferencias, biológicamente evolucionadas, respecto de determinadas clases de hipótesis. Así, incluso si Chomsky tiene razón al sostener que tenemos preferencias innatas por ciertas clases de gramáticas, esto no implica adoptar la visión de Peirce acerca de que la abducción respecto de las hipótesis científicas esté innatamente restringida.
Sólo nuevas investigaciones empíricas determinarán la medida en que debamos postular las preferencias innatas por determinadas clases de hipótesis. Al menos podemos confiar en no aceptar la versión fuerte del [72] innatismo propuesto por Fodor (1975, p. 82). Sostiene que aprender un concepto es aprender su verdadera definición: los hablantes entiende un predicado "P" si y sólo si han aprendido una definición que especifica bajo qué condiciones "x es P" es verdadera. Se sigue que el lenguaje del pensamiento debe ser, por lo menos, tan rico como cualquier lenguaje natural o, también, que no sería posible utilizarlo para aprender la verdadera definición. La discusión acerca del significado en las últimas secciones muestra que ambas instancias en este argumento con débiles. Primero, no hay razón para asociar la comprensión de un concepto con su verdadera definición, dado que el significado proviene de los roles conceptuales que surgen del lugar que ocupa un concepto en diversas reglas y conceptos, no precisamente de las definiciones. Y, segundo, existen varios mecanismos inductivos en un sistema como PI para construir predicados más y más complicados sin tener que haberlos expresado previamente. Fodor supone que el lenguaje del pensamiento está fijado de modo innato, pero hemos visto que aprender los mecanismos que generan nuevas reglas y conceptos puede llevar al lenguaje del pensamiento a mejorarse a sí mismo.
4.6 Limitaciones de PI
PI no tiene medios para interactuar con el mundo real, por lo que cualquier inferencia que realice depende de símbolos preseleccionados para él por el programador. Sus mecanismos para la abducción están super simplificados en varios aspectos.
La combinación conceptual en PI también está limitada al no tomar suficientemente en cuenta el conocimiento de base.
¿Por qué suponer que PI es un modelo preciso del [73] pensamiento humano? Hay al menos un soporte experimental indefinido para los mecanismo de PI acerca de la extensión de la activación y generalización, pero se ha hecho relativamente poco trabajo acerca del proceso psicológico de la abducción y la combinación conceptual.
Pro PI proporciona un comienzo para mostrar cómo procesos tales como la abducción y la combinación conceptual pueden ayudar en la formación de teorías.
4.7. Resumen
Un programa como PI puede proporcionar conocimiento acerca de cómo pueden descubrirse las teorías científicas. La abducción -formación de hipótesis explicativas- es el medio básico par introducir nuevas teorías. Activar reglas en un sistema de solución de problemas, cuyo objetivo sea explicarlas, puede sugerir hipótesis que las expliquen. Nuevos conceptos teóricos pueden formarse por combinación conceptual. El significado se desarrolla en un sistema mediante mecanismos inductivos que establecen funciones conceptuales y no existe dificultad para atribuir tales funciones a conceptos teóricos así como a aquellos cuyos orígenes esté más cercano de la observación.
[74][75] Capítulo 5
Evaluación de la teoría
5.1. Del descubrimiento a la evaluación
El último capítulo describió cómo mecanismos tales como la abducción y la combinación conceptual pueden conducir a la formación de nuevas teorías que pueden explicar reglas generales. Es claro que no queremos aceptar una teoría meramente porque explica algo. Recuerden el terrible chiste acerca del científico que cortó una de las patas de una rana y dijo, "Salta" y la rana saltó. Entonces le cortó otrs dos patas y dijo "Salta" y la rana mal que bien saltó. Finalmente, cortó la pata que quedaba y dijo "Salta", pero la rana no saltó. Consecuentemente, el científico abdujo que las ranas sin patas eran sordas. Claramente, queremos aceptar una teoría sólo si nos proporcional la mejor explicación de la evidencia relevante.
Aunque la expresión "inferencia hacia la mejor explicación" es reciente, originada en Harman (1965), la idea de que las hipótesis han de aceptarse sobre la base de que lo que explican tiene una larga historia, retrocediendo al menos hasta el Renacimiento (Blake, 1960). La mayor debilidad de la afirmación de que la inferencia hacia la mejor explicación es una clase importante de inferencia inductiva es la falta de especificación acerca de cómo determinamos qué hipótesis o teoría es la mejor explicación. Excepto por alguna observación muy breve acerca de elegir una hipótesis que sea más simple, más plausible, que explique más y sea menos ad hoc, Gilbert Harman (1967) sólo dirige el problema hacia su relación con la inferencia estadística. En trabajos posteriores, Harman (1973, 1986) habla vagamente de maximizar la coherencia explicativa al mismo tiempo que minimiza el cambio. Keith Lehrer (1974, p. 165) incluso a remarcado la "desesperanza" de obtener un análisis útil de la noción de una mejor explicación.
Mostraré, sin embargo, que el razonamiento científico actual exhibe un conjunto de criterios para evaluar las teorías explicativas. Los criterios -abarcabilidad (comprensividad) ["consilience"], simplicidad y analogía- proporcionan una amplia base a la justificación de las teorías científicas, acorde con los primeros constructos computacionales de las teorías. Una vez más, el sistema PI proporcionará una ilustración computacional de algunos de los rasgos claves del razonamiento científico [76], sugiriendo respuestas a preguntas tan difíciles como:
1. ¿Cómo establecemos el conjunto de teorías competitivas
que habrán de evaluarse?
2. ¿Cómo establecemos la evidencia que habrá de utilizarse para evaluar las
teorías?
3. ¿Como nos manejamos con situaciones en las que una teoría no explica todo
lo que explican sus competidoras, pero la preferimos de todos modos porque
explica los fragmentos de evidencia más importantes?
4. ¿Qué significa decir que una teoría es más simple que otra?
5.2. Estudios de casos acerca de la elección de teorías
Para comenzar la investigación acerca de la evaluación de la teoría científica, presento ahora tres importantes casos históricos: Darwin sobre la teoría de la evolución, Lavoisier sobre la teoría del oxígeno en la combustión y Fresnel sobre la teoría ondulatoria de la luz. Sólo mencionaré aquellos aspectos de los casos que son de importancia para el actual proyecto de construir criterios para la elección de teorías. Documentación histórica más completa se proporciona en Thagard 1977b). Los casos son aquellos en los que los científicos defendieron explícitamente que sus teorías proporcionaban mejores explicaciones que las teorías competitivas. El Capítulo 7 desarrollará la relación entre los estudios acerca de cómo se hace la ciencia y la cuestión normativa de cómo debe hacerse.
Consideremos primero el largo desarrollo de Charles Darwin acerca de su teoría de la evolución de las especies por medio de la selección natural. En su libro On the Origin of Species, cita una larga serie de hechos que se explican por la teoría de la evolución, pero que eran inexplicables desde la perspectiva entonces aceptada de que las especies fueron creadas por Dios independientemente. Darwin explica hechos relativos a la distribución geográfica de las especies, la existencia de órganos atrofiados en los animales y muchos otros fenómenos. Afirma en la sexta edición de su libro, "Difícilmente puede suponerse que una teoría falsa explicaría, del modo satisfactorio como lo hace la teoría de la selección natural, la gran clase de hechos diversos antes señalados. Recientemente se le ha objetado que ésta es un método peligroso de argumentar; pero este es un método usado para juzgar acerca de los sucesos comunes de la vida y ha sido usado con frecuencia por los principales filósofos naturales" (Darwin, 1962, p. 476). Muchas otras citas podrían darse par mostrar que la argumentación de Darwin en On the Origin os Species consiste en mostrar que su teoría proporciona la mejor explicación para un conjunto de hechos (ver 8.1.2).
Uno de los mayores avances en la historia de la química fue el descubrimiento de Antoine Lavoisier de la teoría del oxígeno de la combustión, que reemplazó la teoría vigente basada en la hipotética sustancia del flogisto. Lavoisier ofreció explicaciones de la combustión, calcinación de metales y otros fenómenos en los que hay absorción de aire. Afirmó, "Deduje [77] todas las explicaciones de un principio simple, que el aire puro o vital está compuesto de un principio que le es particular, que forma su base y al que denominé principio de oxígeno, combinado con la materia de fuego y calor. Una vez admitido este principio, las grandes dificultades de la química parecían disiparse y desvanecerse y todos los fenómenos se explicaban con una sorprendente simplicidad" (Lavoisier, 1862, vol. 2, p. 623). Según la teoría vigente del flogisto, los objetos quemados liberaban la sustancia flogisto, mientras que según Lavoisier, los objetos quemados se combinaban con el oxígeno. El punto principal del razonamiento de Lavoisier es que su teoría podía explicar el hecho de que los cuerpos sometidos a combustión incrementan su peso en vez de disminuirlo. Para explicar el mismo hecho, los proponentes de la teoría del flogisto tenían que formular el supuesto de que el flogisto, que supuestamente salía, tenía "peso negativo". Dado que la teoría del oxígeno explicaba la evidencia sin hacer tal suposición, podía inferírsela como la mejor explicación.
Otros ejemplos de argumentos para la mejor explicación, esta vez en la física, pueden encontrarse en la historia de la teoría ondulatoria de la luz. En su Treatise on Light, Christian Huygens (1962/1690) defendía su teoría ondulatoria de la luz mostrando cómo ella explicaba la propagación rectilínea de la luz, la reflexión, la refracción y algunos de los fenómenos de la doble refracción. La teoría ondulatoria fue eclipsada por la teoría de las partículas de Newton, pero Thomas Young intentó revivir la teoría ondulatoria en tres artículos publicados entre 1802 y 1804. La mayor ventaja de la teoría de Young sobre la de Huygens fue el añadido de la ley de interferencia, que permitió a la teoría explicar numerosos fenómenos de luz coloreada (Young, 1855, vol. 1, pp. 140-191). Finalmente, en una serie de artículos después de 1815, Fresnel atacó la teoría de partículas argumentando que la teoría ondulatoria explicaba los hechos de la reflexión y la refracción al menos tan bien como lo hacía la teoría de partículas y que había otros hechos, implicando la difracción y la polarización, que sólo podía explicar con simplicidad la teoría ondulatoria. Le escribió a Arago, "Así la reflexión, la refracción y todos los casos de difracción, los anillos coloreados en incidencias oblicuas tanto como perpendiculares, la destacable coincidencia entre el espesor del aire y el del agua que producen los mismo anillos; todos estos fenómenos, que requieren tantas hipótesis particulares en el sistema de Newton, se agrupan y se explican por la teoría de las vibraciones y las influencias de los rayos en cada uno" (Fresnel, 1866, vol. 1, p. 36). Por tanto, la teoría ondulatoria debería inferirse como la mejor explicación.
Pueden darse muchos otros ejemplos acerca de la defensa de teorías mediante argumentos acerca de la mejor explicación. William Harvey (1962, p. 139/1628) justificaba su teoría de la circulación de la sangre por lo mucho que explicaba. La teoría general de la relatividad reemplazó a la mecánica newtoniana porque podía explicar más. La teoría de la deriva de los continentes fue considerada primero como una hipótesis salvaje, pero cuando se la asoció con las placas tectónicas se hizo demasiado [78] exitosamente explicativa como para negarla. Como veremos en el capítulo 10, diversas teorías acerca de la extinción de los dinosaurios se han propuesto basadas en su poder explicativo.
5.3. Abarcabilidad ("Consilience")
[...] La noción de abarcabilidad deriva de los escritos de William Whewell (1967/1840). Abracabilidad se propone servir como una medida de cuánto explica una teoría, de modo que podamos usarla para expresar si una teoría explica más de la evidencia que otra teoría. A grandes rasgos, se dice que una teoría tiene abarcabilidad si explica, al menos, dos clases de hechos. [...]
Una mirada más detallada, sin embargo, muestra que el tema es más oscuro de lo que parece. ¿Qué es, por ejemplo, una clase de hechos? [...]
El rasgo más difícil de la noción de abarcabilidad es la noción de una clase de hechos. Whewell también escribe, a veces, acerca de "calidades" ("kinds") de hechos, pero esto sugiere equivocadamente que el problema es ontológico. Pero el problema es meramente pragmático, relativo al modo según el cual, en contextos históricos particulares, el corpus científico está organizado. [...] [79]
[...] Los teóricos que se preocupan más de desarrollar una teoría que de criticarla desatienden los hechos inexplicados. Pero si una nueva teoría entra en escena y tiene éxito al explicar lo que hacia la anterior, así como los hechos previamente inexplicados, entonces, por una cuestión de lógica, la vieja teoría debe atender a los hechos ahora explicados. [...]
No he usado la noción de ley para definir la abarcabilidad, porque no todos los hechos aducidos en favor de las teorías son leyes en un sentido completamente general e irrestricto. Algunos lo son [...]. Pero otros hechos hacer referencia a objetos particulares [...]. es más, en el caso de Darwin y de la psicología actual, por lo general sería mas preciso hablar de hechos que son tendencias o efectos estadísticos, más que leyes. Todos estos, no obstante, son suficientemente generales como para estar representado como reglas de las que se encuentran en PI. [...]
[80] Una teoría abarcativa unifica y sistematiza. Decir que una teoría es abarcativa es decir más que "da cuenta de los hechos" o "tiene una perspectiva amplia"; es decir primero que la teoría explica los hechos y, segundo, que los hechos que explica pertenecen a más de un dominio. Estos dos rasgos diferencian abarcamiento de una cantidad de otras nociones, que se han denominado "poder explicativo", "poder sistemático", "sistematización" o "unificación". [...]
Tras esos intentos está el supuesto de que el poder explicativo puede de algún modo determinarse considerando las consecuencias deductivas de una hipótesis. Pero deducciones como "A, entonces A", así como los ejemplos más complicados expuestos en la sección 3.5.2, muestran que no toda deducción es explicación. Es más, es esencial para la evaluación de [81] el poder explicativo de una hipótesis que lo que se explica se organice y clasifique. [...] Determinar la variedad presupone que un investigador tiene un rico conocimiento de base acerca de las especies de cosas que encuadran los hechos, requiriendo una organización conceptual detallada, semejante a la que se encuentra en PI.
Kitcher (1981) proporciona un valioso complemente a la noción de unificación: una teoría unifica no sólo explicando diferentes clases de hechos, sino que los explica utilizando esquemas de solución de problemas semejantes. [...] Quiero dejar abierta la posibilidad, no obstante, de que no todas las explicaciones provistas por una teoría general están basadas en esquemas, o sea que la unificación por esquemas se considera una rasga asociado de las teorías abarcativas, no una propiedad central.
Hasta aquí, he desarrollado una noción estática de la abarcabilidad de las teorías, la que supone ya dada una totalidad de clases de hechos -la evidencia total. [...] Pero una noción dinámica de la abarcabilidad también debe ser tenida en cuenta al considerar la aceptabilidad de las hipótesis explicativas.
La noción de abarcabilidad de Whewell es esencialmente dinámica. Dice: "La evidencia en favor de nuestra inducción es de un carácter mucho más alto y mucho más fuerte si nos permite explicar y determinar casos de especie diferente a aquellos que fueron considerados en la formación de nuestras hipótesis" (1967, vol. 2, p. 65). Abarcabilidad dinámica puede definirse en función de la abarcabilidad: una teoría es dinámicamente abarcativa si habitualmente es más abarcativa que lo que fue cuando se la propuso por primera vez, o sea, si hay nuevas clases de hechos que ha demostrado que explica. Es difícil formular con precisión una noción comparativa de abarcabilidad dinámica. A grandes rasgos, una teoría es dinámicamente más abarcativa que otra si ha tenido éxito en añadir más a su conjunto de clases de hechos explicados de lo que logran las otras.
El éxito en la predicción con frecuencia puede entenderse como una indicación de abarcabilidad dinámica, dado que la predicción se refiere a temas que son nuevas aplicaciones de la teoría y dado que la predicción es también una explicación. [...] [82]
Aunque la abarcabilidad dinámica se considera con frecuencia más impresionante que la abarcabilidad ordinaria (cf. la noción de un progresivo cambio-de-problema, en Lakatos, 1970), no veo razón para atribuir un valor especial a la dimensión temporal. [...]
La hipótesis o teoría máximamente abarcativa es aquella que explica cualquier hecho. esto se alcanzaría teniendo tal flexibilidad en el conjunto de las hipótesis auxiliares que cualquier fenómeno pudiera caer bajo la teoría. Lavoisier acusó a la teoría del flogisto de tener esta propiedad y la teoría psicoanalítica ha sido acusada con frecuencia de explicar demasiado. Yo quisiera por ello poner una nuevo límite a la abarcabilidad, exigiendo que, para que una teoría tenga abarcabilidad, no sólo debe explicar un rando de hechos, sino que también debe especificar los hechos que no puede explicar. Sin embargo, este requisito es insatisfactorio, porque un modo en que un teoría podría satisfacerlo sería especificando hechos en una campo totalmente diferente; por ejemplo, la teoría psicoanalítica no explica la velocidad de la luz. [...] El límite a estos ajustes depende de que el incremento de la abarcabilidad de una teoría se compense con una disminución en la satisfacción de otros criterios. La simplicidad es el límite más importante a la abarcabilidad.
5.4. Simplicidad
La simplicidad es, con la mayor claridad, un importante factor en los argumentos de Fresnel y Lavoisier. La especie de simplicidad implicada en estos casos tiene poco que ver con las habituales nociones filosóficas basadas en consideraciones sintáticas. Más bien, la simplicidad está pragmática e íntimamente conectada con la explicaciòn.
[83] La explicación de los hechos F por una teoría T requiere también un conjunto de hipótesis auxiliares A y un conjunto de condiciones dadas C. C no es problemático ya que se supone que todos los miembros de C están aceptados, independientemente de T o F. Pero A requiere una consideración detallada. Un hipótesis auxiliar es un enunciado, que no es parte de la teoría original, al que se acepta para explicar uno o una pequeña fracción de los elementos de F. [...]
Ahora podemos decir que la simplicidad es una función del tamaño y naturaleza del conjunto A, necesitada por una teoría T para explicar los hechos F. Esta es la principal noción de simplicidad utilizada por Fresnel y Lavoisier. [...] Estos ejemplos muestran cómo la simplicidad pone un límite a la abarcabilidad: una simple teoría abarcable no sólo debe explicar un rango de hechos, debe explicarlos sin hacer una multitud de supuestos de aplicación limitada .
Una hipótesis ad hoc es la que no sirve para explicar más fenómenos que el limitado rango para explicar los cuales había sido introducida. Por tanto, una teoría simple es aquella que tiene pocas hipótesis ad hoc. Pero lo "ad hoc" no es una noción [84] estática. No se puede condenar una teorìa por introducir una hipótesis para explicar un hecho particular, ya que todos los teóricos emplean tales hipótesis. Las hipótesis sólo pueden criticarse si el avance de las investigaciones fracasa tanto pra descubrir nuevos hechos que ayudan a explicar o para encontrar evidencias más directas a su respecto [...]. Además, un supuesto auxiliar no se considerará ad hoc si lo compartes las toerías competitivas.
Esto nos proporciona una noción comparativa de la simplicidad. Sea ATi el conjunto de hipótesis necesarias para que Ti explique el conjunto de hechos F. Se decide entre T1 y T2 comparando AT1 y AT2. Pero, ¿cómo se hace esto? El tema no es nítidamente sintáctico, ya que cualquier AT puede considerarse que tiene un único miembro, reemplazando sus elementos por la suma de esos elementos. Ni podemos usar la relación de subconjuntos como lo hacemos al comparar conjuntos de clases de hechos explicados, porque es muy posible que AT1 y AT2 no tengan miembros en común. Los argumentos de Fresnel y otros sugieren hcer una comparación cualitativa, caso por caso. [...] Así, la simplicidad comparativa de dos teorías sólo puede establecerse mediante el examen cuidadoso de los supuestos introducidos en las diversas explicaciones que ofrece. Como se ha destacado con frecuencia, la simplicidad es muy compleja. Véase 5.5.3 para una descripciòn de cómo PI establece la simplicidad.
Este análisis de la simplicidad esclarece dos temas expuestos con anterioridad: la predicción y la unificación. ¿Por qué a algunos filósofos les impresiona que una teoría formule predicciones acerca de la observación de algunos nuevos fenómenos, más que que las formule acerca de los ya conocidos? [...] Yo sostengo que la principal razón por la que la predicción de nuevos fenómenos parece tan importante es que tales predicciones puede ser un signo de explicaciones simples. Al hacer una predicción, no se tiene la oportunidad de ajustar la teoría a un resultado ya conocido, mediante hipotesis auxiliares. Al usar sólo la teoría y los supuestos auxiliares ya conocidos, se predice un reusltado futuro sin oportunidad para ajustes que dependen de la predicción. Por el contrario, la explicación después del hecho puede hacer numerosos supuestos especiales para que el [85] resultado se derive de la teoría. Contrariamente al enfoque de Popper (1959), las predicciones no deben valorarse por lo que pueden proporcionar acerca de la falsación; el rechazo de una teoría requiere mostrar que una teorìa alternativa copnstituye una explicación mejor. Más bien, las predicciones exitosas se deben evaluar como signos de la simplicidad de una toerìa, mostrando que sus explicaciones no reuieren añadidos post hoc. Las explicaciones simples es más posible que proporcionen unificaciones, ya que la ausencia de hipótesis añadidas significa que las explicaciones usan los recursos existentes de la teoría, incluidos los esquemas explicativos establecidos, incrementando así el grado de unificación encontrado en la teoría.
El precedente desarrollo de la simplicidad es superficialmente semejante al propuesto por Elliot Sober (1975). Sobre define la simplicidad como informatividad, en la que una hipótesis H es más informativa que H' con respecto a la pregunta Q, si H requiere menos extra-información que H' para responder a Q. [...] Lavoisier y Fresnel mostraron no interesarse en la complejidad sintáctica de las explicaciones dadas por sus oponentes: la contidad de condiciones iniciales requeridas es irrelevante. Lo que importan son los supuestos especiales formulados para explicar clases particulares de hechos. Por lo tanto, la simplicidad va más allá de la noción sintáctica de informatividad desarrollada por Sober. Vimos al exponer la abarcabilidad que la individualización de clases de hechos requiere la consideración de la historia del estudio y las estructuras cognitivas de los estudiosos.
Al margen de comparar los conjuntos de hipótesis auxiliares AT1 y AT2 , también se puede enjuiciar la simplicidad comparando T1 y T2 . Pero no logro ver cómo puede hacerse en general. La cantidad de postulados en una teoría parece aportar poco en cuanto a su aceptabilidad; lo que importa es que cada postulado se use par la explicación de clases de hechos diferentes. [...] Sin embargo, T1 y T2 pueden comparase a otro nivel; el de le economía ontológica. Lavoisier sugiere que teoría del flogisto es menos simple que la teoría del oxígeno, ya que asume la existencia de otros sustancia, el flogisto. De modo semejante, la hipótesis creacionista es ontológicamente más compleja que la teoría de la evolución. [...] [86]
T1 es ontológicamente más económica que T2 si T1 asume la existencia de entidades que T2 no asume. El criterio de la economía ontológica es subsidiario de los de abarcabilidad y simplicidad porque la navaja de Occam nos aconseja no multiplicar las entidades más allá de la necesidad. [...]
Pero la simplicidad, ejemplificada por las exposiciones de Lavoisier y Fresnel, es importante. Las teorías no deben alcanzar la abarcabilidad a expensas de la simploicidad mediante el uso de hipótesis auxiliares. [...] La inferencia hacia la mejor explicación es inferencia hacia una teoría que mejor satisfaga los criterios de abarcabilidad y simplicidad, así como un tercero, la analogía. Sin embargo, antes de dicutir la analogía, quiero desarrollar más las nociones de abarcabilidad y simplicidad describiendo cómo el programa PI las toma en cuenta al evaluar la mejor explicación.
5.5. Inferencia hacia la mejor explicación en PI
[...] Los formalismos apropiados para desarrollar un modelo más completo de la teoría de la evaluación puede venir, no obstante, de la inteligencia artificial. [...]
[87] 5.5.1 Teorías competitivas y evidencia
Siguiendo a Hempel (1965) me refiero al hecho o generalización que hay que explicar como un explanandum (plural explananda). Cuando PI encuentra una explicación, registra el éxito añadiendo lo que se explicó a la lista de los explananda de la hipótesis explicativa y añadiendo la hipótesis a la lista de los explicadores del explanandum. [...] Tras cada logro explicativo de una teoría T1, PI se pregunta si T1 es la mejor explicación. Responder a esto requiere comparar T1 con las teorías explicativas alternativas respecto de la evidencia total disponible.
¿Pero, qué hace que una teoría sea una alternativa de T1 y cuál es la evidencia total que debe tomarse en cuenta). [...] PI usa un simple algoritmo para compilar listas de teorías alternativas y de evidencia relevante, a partir de explicaciones ya alcanzadas. Mira la lista de explananda explicadas por T1 y comprueba qué otras teorías se usaron para explicarlos. Toda T2 que explica alguno de los explananda de T1 es una competidora de T1. [...] Cuando una búsqueda continua no muestra nuevos competidores o explananda, PI llega a la conclusión de que tiene un conjunto completo de competidores y evidencia.
[...] PI atiende a lo que se encontró para explicar qué. Como vimos en el capítulo 3, la explicación desde una perspectiva computacional puede considerarse con una proceso histórico cuyos resultados están almacenados en el sistema de procesamiento, no como una relación [88] abstracta entre teorías y explananda. [...]
De modo semejante, los científicos no toman en cuenta todas las teorías y explananda posibles cuando evalúan las teorías. [...] En ciencia, no obstante, hay también una importante dimensión social, implicando la interacción entre los científicos y las fuerzas sociales reguladoras tales como la revisión entre pares.
5.5.2 Abarcabilidad en PI
[Doy un salto en la continuidad de la traducción, porque me interesa tener pronto disponible la traducción del Capitulo 7. Me comprometo formalmente a completar lo que ahora dejo de lado.]
[112][113] Capítulo 7
De lo descriptivo a lo normativo
7.1. El carácter normativo de la filosofía
El capítulo anterior proporcionó descripciones acerca de cómo se desarrolla el conocimiento científico a través de los procesos de resolución de problemas, descubrimiento y evaluación de las teorías. Estas descripciones están naturalmente vinculadas a los campos de la psicología cognitiva, la inteligencia artificial y la historia de la ciencia. Pero la filosofía ha tratado siempre, no sólo con lo que es, sino también con lo que debe ser, con lo normativo al igual que con lo descriptivo. La lógica, la filosofía de la ciencia y la epistemología son, por lo general, campos normativos, que proporcionan las evaluaciones así como las descripciones de los métodos para alcanzar el conocimiento. [...]
Tradicionalmente, los filósofos han visto dos maneras de justificar los modos de razonar. El enfoque racionalista intenta descubrir los principios del razonamiento mediante reflexiones a priori acerca de las propiedades necesarias de la mente racional. Pero la proliferación de lógicas formales y el estudio empírico de las clases de razonamiento humano han destruido la plausibilidad de la afirmación de que existe un modo esencial según el cual los seres racionales piensan y deben hacerlo. Hoy día es más habitual decir que los cánones normativos de la lógica y la filosofía de la ciencia no tienen que ser en absoluto. Paul Feyerabend (975) [114] resume su anarquismo epistemológico en la frase: todo marcha. Richard Rorty (1979) exhorta a los filósofos a abandonar la epistemología fundacional por la "edificación" hermenéutica. El pesimismo de Feyerabend y de Rorty procede de los fracasos de la filosofía analítica y de la filosofía positivista de la ciencia en lograr que sus programas acerca del uso de las técnicas del análisis lógico establezcan un fundamento claro del conocimiento, incluido el conocimiento científico. ¿Existe una alternativa a la depresión positivista?
Sí: podemos llegar a principios normativos del razonamiento reflexionando sobre descripciones acerca de cómo cotidiana y efectivamente trabaja el razonamiento científico. Tal reflexión no deriva lo normativo de lo descriptivo; no existe no existe una deducción inmediata de necesidad de esto. Sin embargo, los estudios descriptivos contribuyen substancialmente al establecimiento de los principios normativos. [...]
Para mostrar cómo conclusiones normativas pueden extraerse de temas descriptivos, consideraré varias áreas en las que los filósofos han encontrado que lo descriptivo es relevante para lo normativo. Después de una breve crítica de la bien conocida exposición de Nelson Goodman sobre la justificación de la inducción, examino tres casos fructíferos del desarrollo de los principios normativos basados en lo descriptivo. [...]
7.2 Goodman: conclusiones normativas a través del equilibrio reflexivo
Hume (1888) plantea la escéptica pregunta de si el razonamiento inductivo desde la evidencia hacia conclusiones más generales puede justificarse en algún caso. Nelson Goodman (1965) propuso una valiosa disolución del problema de Hume acerca de la inducción. Goodman sugirió que los principios de la inferencia inductiva, al igual que los principios de la inferencia deductiva, se justificaban meramente por la conformidad con la práctica inferencial aceptada. Goodman escribe: "El punto consiste en que las reglas y asimismo las inferencias particulares se justifican poniéndose de acuerdo las unas con las otras. Una regla se corrige si produce una inferencia que no queremos aceptar; una inferencia se rechaza si viola una regla que no queremos corregir. El proceso de justificación consiste en el delicado proceso de hacer mutuos ajustes entre reglas e inferencias aceptadas; y en el acuerdo alcanzado radica la única justificación necesitada por ambas" [...] Posteriormente, John Rawls (1971) propuso que [115] los principios éticos podrían establecerse mediante un método semejante, con el logro de lo que llamó "equilibrio reflexivo" entre los principios de la moral y los juicios morales individuales. [...]
Stich y Nisbett (1980) mostraron que la propuesta de Goodman era demasiado liberal. [...] Stich y Nisbett proponen que las preguntas acerca de la justificación pueden responderse tomando en consideración los equilibrios reflexivos de los expertos inferenciales. [...]
7.3 Filosofía histórica de la ciencia
Recientemente, muchos filósofos de la ciencia cambiaron los métodos de reconstrucción lógica introducidos por el Círculo de Viena por métodos que implicaban el estudio detallado de los ejemplos históricos o contemporáneos de la práctica científica (Laudan, 1977). [...] el enfoque histórico considera a la filosofía de la ciencia con una disciplina empírica (Hausman, 1981). Una cuidadosa atención debió ponerse en lo que los científicos hacen efectivamente, y las prescripciones acerca de lo que el método científico debe alcanzar se fundamentarían en la efectiva práctica. El manifiesto implícito de este enfoque fue la Estructura de las revoluciones científicas, publicado inicialmente en 1962. [116] podemos usar los estudios históricos para generar principios metodológicos cuyo influjo puede extenderse normativamente hasta cubrir la práctica general de la ciencia. ¿Pero cómo trabaja?
Considérese primero la naturaleza de la evaluación de las teorías, que puede proporcionar la primera grosera aproximación a la selección de los principios lógicos. La discusión acerca de la evaluación de las teorías, en el capítulo 5, sugiere que la elección de teorías se basa en métodos que son comparativos, a grandes rasgos (coarse-grained) y dinámicos. [...] Puede esperarse que la afirmación de los estándares normativos en la filosofía de la ciencia, de la ética y de la lógica sean también comparativos, a grandes rasgos y dinámicos.
Pero hacer filosofía histórica de la ciencia es en muchos aspectos diferente de hacer ciencia empírica. [...] Al hacer ciencia empírica, puede estudiarse un fenómeno determinado porque se lo considera representativo de un amplio rango de fenómenos, pero no hay asociación normativa. En la filosofía histórica de la ciencia, por otra parte, los estudios de casos adquieren significado filosófico por la creencia básica de que científicos tales como Galileo, Newton y Darwin conocían, por lo general, lo que estaban haciendo.
[117] Se reconoce que existen muchas trampas. [...] No suponemos que la efectiva práctica de incluso un acreditado científico debe tomarse siempre como normativamente significativa. [...] Las evaluaciones filosóficas retrospectivas de piezas del trabajo científico pueden cambiar en el tiempo según evolucionan las teorías filosóficas y las concepciones científicas. Así, la filosofía histórica de la ciencia se basa inevitablemente en la historia filosófica de la ciencia. La historia filosófica de la ciencia no es, sin embargo, una empresa arbitraria, ya que también la historia filosófica debe sentirse limitada por los enunciados efectivos de los temas de investigación. [...]
La filosofía histórica de la ciencia es comparativa porque se debe reflexionar acerca de cuál de entre varias metodologías describe y explica mejor lo que ocurre en un caso concreto. Es a grandes rasgos porque no se trata de dar cuenta deductivamente de un listado general de prácticas científicas, sino que se trata de explicar una cantidad restringida de prácticas consideradas históricamente significativas. Y es dinámica porque un criterio que habrá de utilizarse para evaluar un informe filosófico de la metodología se refiere a en qué medida el informe conduce a un subsiguiente trabajo histórico de esclarecimiento. [...]
La filosofìa histórica de la ciencia también puede beneficiarse con la reflexión acerca de la mala ciencia. Mi exposición en el capítulo 9 apunta a iluminar la diferencia [118] entre la ciencia y la seudociencia, tomando en cuenta algunos casos de seudociencias, en especial la astrología y el creacionismo. [...]
Quiero resumir ahora los elementos de la relación descriptivo/normativo en la filosofía histórica de la ciencia que pueda comprobarse aplicable a la pregunta general acerca de la importancia de lo descriptivo en lo normativo. El resultado es un tosco esquema titulado "FHC", por filosofía histórica de la ciencia:
FHC
1. Se seleccionan casos de efectiva práctica científica [...].
2. Se desarrollan estudios de casos que describen la práctica científica.
3. Se supone [...] que los científicos generalmente han tenido éxito en alcanzar los objetivos epistemológicos de la ciencia.
4. Por tanto, los efectivos métodos de los científicos en nuestros estudios de casos son, al menos, una aproximación a lo que los métodos deben ser. [...]
5. Se reflexiona filosóficamente acerca de los métodos encontrados en los estudios de casos, desarrollando los modelos normativos más complejos, los que pueden aplicarse a otros estudios de casos.
[...] La historia y la filosofía de la ciencia pueden verse como parte de un sistema dinámico mejor representado, no por una secuencia de pasos, sino por un proceso de retroalimentación como en la figura 7.1. Las conclusiones metodológicas se alcanzan tras los lazos históricos/metodológicos repetidamente recorridos.
[119] 7.4 Equilibrio reflexivo amplio
John Rawls (1971) recomendó un método ético destinado a alcanzar un "equilibrio reflexivo" entre los juicios morales particulares y los principios morales generales. Norman Daniels desarrolló el método:
"el método del equilibrio reflexivo amplio es un intento para producir coherencia en un triple conjunto ordenado de creencias sostenido por una persona determinada, a saber, (a) un conjunto de juicios considerados morales, (b) un conjunto de principios morales y (c) un conjunto de relevantes teorías de base... Proponemos conjuntos alternativos de principios morales que tiene diversos grados de "encaje" con los juicios morales. No adquirimos simplemente el mejor encaje de principios con juicios, lo que nos daría sólo un equilibrio estricto. En lugar de ello, proporcionamos argumentos filosóficos tendientes a producir la fuerza o debilidad relativas de los conjuntos alternativos de principios (o conceptos morales competitivos)."
Como con la elección de la teoría científica y la filosofía histórica de la ciencia, tenemos aquí un método que es comparativo, de granulado grueso y dinámico. Los [120] juicios morales particulares son revisables y no muestran en ello una gran diferencia con la evidencia empírica usada para evaluar las teorías científicas.
Pero hay una diferencia en grado: los juicios morales son o debieran ser más corregibles. La filosofía histórica de la ciencia proporciona un caso intermedio de corregibilidad.
Un aspecto de gran importancia de la caracterización de Daniels es el papel de (c) un conjunto de teorías de base. La coherencia debe alcanzarse no sólo entre los juicios morales y los principios, sino también con las teorías relativas a materias tales como la naturaleza de los seres humanos y de la sociedad.
[121] La mayoría de los teóricos de la ética acepta el principio de que "debe" implica "puede", de modo que si resulta físicamente imposible para un agente realizar determinada acción, entonces, debe rechazarse el principio moral que dice que el agente tiene que realizarla.
Intentemos esquematizar el modelo para obtener conclusiones normativas basadas en la descripción de Daniel del equilibrio reflexivo amplio. se lo llamará ERA:
ERA
1. Tenemos un conjunto de juicios morales particulares acerca de lo que es
correcto o equivocado, seleccionado por la esperada libertad respecto del error.
2. Postulamos una cantidad de principios morales generales que explican y
justifican los juicios particulares.
3. Intentamos acceder a un conjunto de creencias máximamente coherente,
consistente no sólo en juicios y principios morales, sino también tomando en
cuenta nuestras teorías de base, en especial las concernientes a las
limitaciones psicológicas.
4. Alcanzamos un estado de equilibrio reflexivo y concluimos que la aceptación
de los principios morales en el conjunto final de creencias está justificado.
[122] 7.5 HFC, ERA y la importancia de la psicología para la lógica.
El trabajo empírico reciente en psicología muestra numerosas discrepancias sistemáticas entre la práctica inferencial popular y las normas lógicas aceptadas. [123] Tales discrepancias producen tres posibles respuestas:
1. La gente es
estúpida. Simplemente fracasa al seguir las reglas inferenciales normativamente
apropiadas.
2. Los psicólogos son estúpidos. Han fallado al tomar en
cuenta todas las variables que afectan las inferencias humanas y una vez que se
tomaron en cuenta todos los factores resultó posible mostrar que la gente
seguía, en realidad, las reglas apropiadas.
3. Los lógicos son estúpidos. Afirman el comportamiento
inferencial de los pensadores humanos contra el conjunto equivocado de los
estándares normativos.
En esta discusión asumo la posición igualitaria de que todos llegan a ser estúpidos parte del tiempo. El problema es establecer una metodología para mediar entre el comportamiento inductivo de la gente, las descripciones de los psicólogos de este comportamiento y los principios normativos de los lógicos utilizados para juzgar lo adecuado del comportamiento inferencial.
7.5.1 Limitaciones de la HFC
HFC no proporciona la metodología requerida. Se supone que el pensamiento científico de los sujetos (seleccionados) es ejemplar; adquirimos la garantía de que nuestros científicos estrella sabían lo que estaban haciendo. Cuando los psicólogos nos dicen que la gente con frecuencia no toma en cuenta los fenómenos de regresión, no suponemos que saben lo que están haciendo.
Pero tampoco podemos encontrar expertos en comportamiento inferencial general que sean análogos a nuestros científicos ejemplares. Necesitamos distinguir entre dos clases de expertos: aquellos que son expertos en realizar una tarea y aquellos que son expertos en decir explícitamente cómo debe realizarse una tarea. En lógica, no tenemos tan claro un conjunto de gente acreditada como expertos en su práctica, independientemente de sus afirmaciones.
[124] Podemos suponer que con respecto a la inferencia deductiva podríamos tomar a los matemáticos como nuestros expertos prácticos, con respecto a la inferencia inductiva tenemos los estadísticos y con respecto a la inferencia práctica podríamos tomar gerentes de alto nivel. Pero en todos estos casos, l práctica está severamente infectada por concepciones filosóficas.
7.5.2 Importancia del ERA con respecto a la Psicología y a la Lógica
[125] La aplicación del ERA
al caso psicología/lógica sugiere que deberemos esforzarnos pos alcanzar el
equilibrio reflexivo entre los cuatro siguientes factores:
a. práctica inferencial común
b. principios lógicos normativos
[126] c. teorías de base acerca de las capacidades y limitaciones cognitivas de
los seres humanos, y
d. concepciones de base acerca de los objetivos del comportamiento inferencial
pero, además,
e. teorías filosóficas de base
7.5.3 ¿Equilibrio reflexivo estricto?
Cohen (1981a) afirma sin desarrollarlo que el caso psicología/lógica implica un equilibrio reflexivo estricto. Compara el caso de encajar los principios lógicos con la práctica lógica con inventar una gramática que encaje con la práctica lingüística de una población. Este último es en realidad un caso de equilibrio reflexivo estricto: sólo se tiene en cuenta el ajuste entre principios y práctica y las teorías de base no juegan ningún papel. Pero al construir un conjunto de principios lógicos estamos haciendo mucho más que simplemente proyectarlos sobre la práctica real. La práctica puede mejorar. El lógico tiene que desarrollar un conjunto de principios que sea inferencialmente óptimo dadas las limitaciones cognitivas de los razonadores. Esto requiere la referencia a teorías psicológicas y filosóficas de base y a los objetivos del comportamiento inferencial. Por tanto, los principios lógicos sólo pueden alcanzarse mediante un proceso de equilibrio reflexivo amplio.
7.6 De la psicología a la lógica: criterios relativos a los sistemas inferenciales
7.6.1 Primera aproximación: DPL
El siguiente modelo sugiere un posible procedimiento para intentar resolver las diputas acerca de los principios normativos
DPL
1. Realizamos estudios empíricos para describir el comportamiento inferencial.
2. Generamos conjuntos de principios lógicos que explican y justifican ese
comportamiento inferencial.
3. Cuando el comportamiento inferencial se desvía de las normas lógicas, tomamos
en cuenta si son necesarias nuevas normas o si podemos revisar el comportamiento
inferencial para ponerlo en línea con las normas existentes.
4. Esta consideración depende de algún modo de desarrollar un conjunto
máximamente coherente de creencias acerca del efectivo comportamiento de la
gente, su comportamiento óptimo dadas sus limitaciones cognitivas y los
objetivos del comportamiento inferencial y los resultados filosóficos de base.
5. Los principios lógicos entre el conjunto máximamente coherente de creencias
han de ser evaluados para su justificación.
[128] Por analogía con ERA, repetidamente ajustamos la práctica y los principios lógicos a la luz de las teorías de base, hasta alcanzar el equilibrio reflexivo; entonces los principios alcanzados en el estado de equilibrio son "producidos" como normativamente correctos. En la descripción lineal de DPL, debemos preguntar qué es llegar al paso 4 y lograr un conjunto de creencias "máximamente coherente". Sin dar cuenta de cómo evaluar la coherencia entre práctica, principios, objetivos y teorías de base, DPL tendría un pequeño contenido.
7.6.2 Criterios para la coherencia
Un sistema inferencial es una matriz de cuatro elementos: principios normativos, descripciones de práctica inferencial, objetivos inferenciales y teorías filosóficas y psicológicas de base. ¿Cómo afirmamos la coherencia de tal sistema? O más importante, ¿cómo podemos decir que un sistema es más coherente que otro? Propongo tres criterios principales: solidez, adecuación y eficacia. Un sistema es sólido (robustness) si sus principios normativos dan cuenta de la práctica inferencial en un amplio rango de situaciones.
NOTAS de los traductores
* La traducción no es completa. Se han seleccionado las partes que permitan seguir el hilo del desarrollo fundamental que va realizando P. Thagard.
1 Los números, romanos para el Prefacio y arábigos en el resto, establecen la página del texto original donde se encuentran los textos traducidos.